【현대물리학】 복소수

다음과 같은 2차 방정식을 고려한다면, 근의 공식을 이용해 아래와 같은 근을 구할 수 있다.

근의 공식을 적용한 결과 음수의 제곱근이 나오는 데, 어떠한 크기의 양수든 음수든 제곱을 취하면 모두 양수 값만이 나오기 때문에 √(-36)은 일반적인 실수범위 값이 아니라고 생각할 수 있다. ⇒ 실수범위의 수에 제곱을 취하는 경우 결코 음수가 나올 수 없다. 때문에 제곱하여 음수가 나오는 새로운 수체계가 필요하다.

- 어떠한 음수의 제곱근도 허수를 통해 정식으로 표현할 수 있다.

허수의 개념을 도입하면 위의 2차 방정식에서 2개의 근을 얻을 수 있다.

위의 두 근처럼 a+bi의 형태를 가진 수를 복소수(complex numbers)라고 부른다.
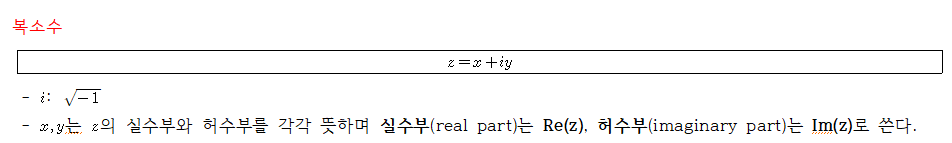
복소수와 복소함수의 일반적 성질은 양자역학에서 매우 자주 사용하는 수학적 개념 중 하나이다.
복소수의 성질

5. 복소수와 공액 복소수를 곱하면 의 제곱절대치가 나타난다. ⇒ 제곱치 혹은 제곱 절댓값이라고도 부른다.

- i^2=-1의 관계식을 활용한다.
- 제곱 절대치는 실수(real number)범위이다.

PROOF. 복소수의 역수

복소수 극좌표

복소평면(아르강 도표, complex plane, Argand diagram; 프랑스의 아마추어 수학자 아르강(Robert Argand, 1768~1822)이 복소수를 기하학적으로 해석하는 방법으로 제시한 도표): 복소수는 복소평면이라는 평면상의 점으로 나타낼 수 있다.
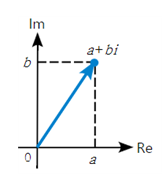
- Re는 x-, Im은 y-상에 나타내고 화살표의 길이와 끼인각 φ는 점의 극좌표를 나타낸다. ⇒ 각도는 일반적인 극좌표와 마찬가지로 +x-에서 반시계 방향으로 측정하며, 반시계 방향에 대해 양의 부호를 가진다.

위의 관계식은 극좌표를 카테시안 좌표로 바꾸는 유용한 방법으로, 길이가 r=1인 경우 다음과 같이 다시 정리된다.

PROOF. 오일러의 식

스위스의 수학자이자 물리학자인 오일러(Leonhard Euler, 1707~1783)가 고안한 식으로 복소수의 성질을 이용해 다음과 같이 유도할 수 있다.
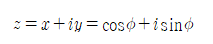
이 식을 각도에 대해 미분하면 다음 식이 나온다.

then,

이후 위의 식을 대수적으로 변형한 후, 각각에 대해 적분한다.


오일러 식의 허수가 -i이면 오일러 식은 다음과 같이 변한다.

이들을 종합해 극좌표 꼴로 나타낸 복소수 식은 아래와 같이 다시 쓸 수 있다.
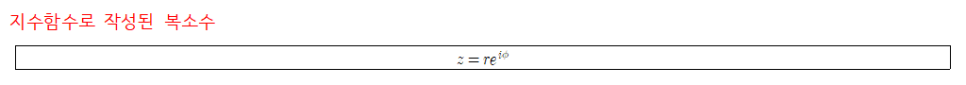
드무아브르 정리
복소수 이론 중 매우 중요한 결과 중 하나로 드무아브르 정리(De Moivre's theorem; 프랑스 출신의 영국 수학자 드무아브르(Abraham de Moivre, 1667~1754)가 고안한 기본정리로 복소수와 삼각함수를 연결했다.)가 있다.

▶각각의 식은 n에 적절한 수를 넣어 증명할 수 있다.