고급물리학/고전역학
[물리학-고전역학] 다변수 함수와 편미분 | Multivariable Functions and Partial Derivatives
herald-lab
2023. 10. 24. 14:35
728x90
반응형

다변수 함수(multivariable functions): 둘 이상의 독립변수를 갖는 함수
- 다변수 실함수와 다변수 복소함수를 포함함
- 물리학에서 발견할 수 있는 대표적인 예는 기체의 압력을 들 수 있다. ⇒ 기체 압력(p)은 부피(V)와 온도(T)에 동시에 영향을 받는다.
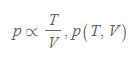
또한 기하에서 원통(실린더, cylinder)[그림 1]의 부피는 다변수 함수에 해당한다.

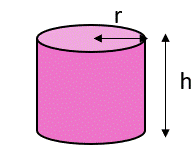
- 의미: 원통의 부피는 뚜껑의 반지름과 원통의 높이에 의존한다.
- 종속변수는 부피(V)이다.
- 독립변수는 원통의 반지름 r과 원통의 높이 h로 V(r, h)로 부피 식을 표현할 수 있다.
원통의 부피는 두 개의 독립변수에 의해 결정되므로, 이변수 함수라고 한다.
편미분
Partial Derivatives
미분적분학에서 편미분이란 둘 이상의 변수를 갖는 함수의 독특한 미분법으로, 이려 변수들 중 하나의 변수에 대해서만 미분하고, 나머지 값은 상수로 취급하는 것이 특징이다. cf. 전미분(total derivative)
- 미분기하학에서 특히 자주 사용하는 개념으로, 함수 f(x, y, z, ...)에서 x에 대한 편미분은 아래와 같이 표기한다.
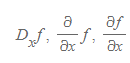
1계 편미분함수(first partial derivative)
만약 z=z(x, y)일 때, z의 1계 편미분함수는 다음과 같이 표현한다.
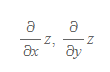
- ∂z/∂x: x에 대한 미분함수를 구할 때, 다른 독립변수인 y는 일정하게 둔 채 x만 미분시킨다. y는 상수로 취급한다.
- ∂z/∂y: y에 대한 미분함수를 구할 때, 다른 독립변수인 x는 일정하게 둔 채 y만 미분시킨다. x는 상수로 취급한다.
어떤 특별한 한 점 (x_1, y_1)에서 편미분 함수 ∂z/∂x를 계산할 때, 일변수 함수에서와 같이 아래처럼 표현한다.
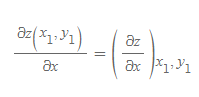
예제
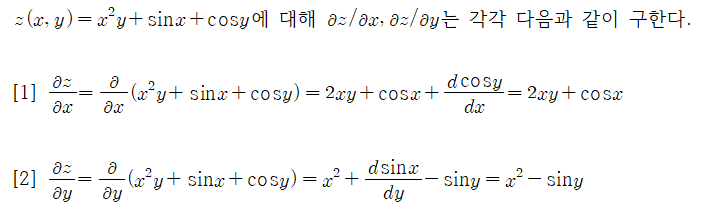
- [과정 1]에서 y는 마치 상수와 같이 취급하여 독립변수 x에 대해서만 미분 법칙을 적용한다.
- [과정 2]에서 x는 마치 상수와 같이 취급하여 독립변수 y에 대해서만 미분 법칙을 적용한다.
고계미분
Higher Order Derivatives
기존의 일변수 함수가 고계미분 된 것처럼 다변수 함수 역시 2계 및 고계미분(함수)을 취할 수 있다.
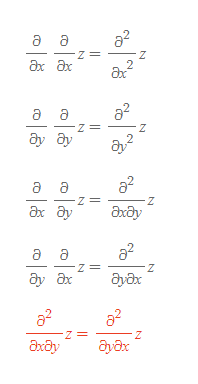
- 위 식의 마지막 빨간색 식을 '고계미분함수정리'라 한다. ⇒ 각각의 독립변수에 대해 종속변수를 1차 미분한 값은 그 순서와 상관없이 결과 값이 항상 같다.
- 또는 편미분의 교환법칙으로 라이프니츠의 적분 규칙을 이용해 증명이 가능하다.
예제

1차 편미분과 고계미분 기법을 활용해 공학에서 자주 쓰이는 편미분 방정식(partial differential equation, PDE)을 계산해보도록 하자.
728x90
반응형