[물리학-고전역학] 운동량과 충격량 | Momentum and Impulse

운동량에 관하여
About the Momentum
운동량(momentum): 물체의 운동을 지속시키게 하는 물리량, 운동하는 물체의 경우 운동량 때문에 물체는 정지 상태에 도달하기 어렵다.
- 라틴어 movimentum이 어원으로, 의미는 '움직임'이다.
- 초기의 운동량은 임페투스(impetus)라는 개념에서 출발했으며, 수 세기 동안 그 개념이 발전되면서, 현재 물리학에서는 '운동의 세기'의 개념으로 물체의 질량 × 물체의 속도로 정의한다.
물체의 선운동량 | Linear Momentum
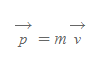
■
질량이 m_1, m_2인 두 입자가 속도 v_1, v_2로 동시에 움직이는 고립계를 떠올려보자.
- 계는 고립계이므로, 한 입자 A에 작용할 수 있는 유일한 힘은 다른 입자 B가 그 입자 A에 작용하는 힘 뿐이다.
- 뉴턴의 운동 제 3법칙 적용
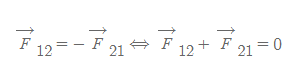
- 각 입자에 작용하는 '힘'은 m(벡터 a)로 고쳐 쓸 수 있다.
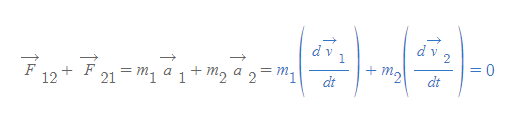
- 두 입자의 질량이 일정하다면 이들을 미분 연산에 집어넣을 수 있다.
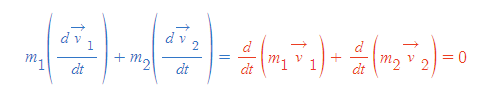
- m(벡터 v)의 시간에 대한 도함수가 0이므로, 두 mv의 합은 상수여야 한다. ⇒ 고립된 입자계에서 각 입자에 대한 m(벡터 v)의 합이 보존된다.

여기서 상수 값으로 보존되는 공통의 mv를 입자의 선운동량(linear momentum)이라 정의한다.
- 방향: 물체의 속도방향과 일치[그림 1]
- 운동량은 벡터량이다.
- 단위: [kg·m/s]
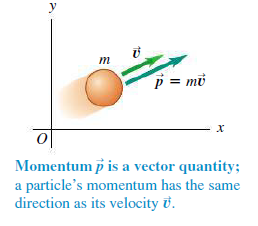
- 같은 속도라 할지라도, 질량이 큰 물체일수록 물체의 운동량은 더욱 크다. 그리고 운동량은 운동의 세기이므로 질량이 큰 물체일수록 운동의 세기도 더 클 것이다.
힘에 대한 새로운 정의
운동량을 가지는 물체의 질량은 일반적으로 보존된다.
Newton의 운동법칙에 따라 알짜힘을 다음과 같이 적을 수도 있다.
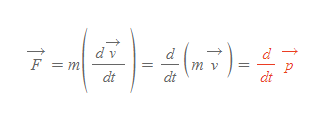
운동량과 힘의 관계식 | Newton's Second Law for a Particle
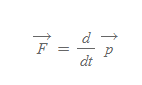
■
- 의미: 뉴턴의 운동 제2법칙의 일반화된 표현 ⇒ (외부의) 힘에 의해 물체의 시간 당 운동량이 변화한다.
- 이 관계식은 질량이 보존되는 경우를 가정해 유도되었지만, 질량이 변하는 경우에도 아래와 같은 식으로 힘을 분석할 수 있다.
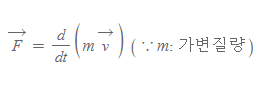
고립계에서의 운동량
고립된 입자계에서 각 입자에 대한 m(벡터 v)의 합이 보존됨을 아래와 같이 표현하자.
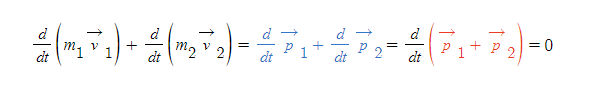
- 위 식에서 빨간색 부분은 총 운동량으로 총 운동량은 각각의 입자가 가진 운동량의 벡터합이다. 총 운동량은 '어떤 한 시점'에서의 각각의 입자가 가진 운동량의 전체 벡터합으로 해석된다. 벡터량이므로 방향 역시 고려된다.
- 전체 운동량은 시간에 대한 도함수가 0이므로 총 운동량 값은 항상 일정한 상수이다.
운동량 보존법칙 | Conservation of Momentum for an Isolated System
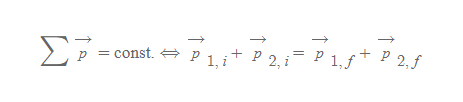
■
- 의미: 두 입자(고립계 조건)가 가진 초기 운동량의 벡터합과 나중 운동량의 벡터합은 항상 같다.
- 고립계 모형의 운동량: 고립계에 있는 두 개 이상의 입자가 상호작용할 때, 이들 계의 전체 운동량은 항상 일정한 값을 취한다.
힘의 종류 및 특성(보존력 여부, 일정한 크기)과는 무관하게 계 내에서 항상 성립한다. ⇒ 힘들이 계의 내부에 존재할 때, 힘의 특성과는 상관없이 운동량 보존법칙은 항상 성립한다.
비고립계에서의 운동량
Momentum for a Non-isolated System
비고립계: 에너지가 계의 경계를 통과할 수 있는 계
- 비고립계는 다시 두 가지로 세분할 수 있다.
- 에너지와 물질이 모두 통과하는 계를 열린 계(opened system)라고 정의한다.
- 에너지는 통과하지만 물질은 통과하지 못하는 계를 닫힌 계(closed system)라고 정의한다.
힘의 충격량
[1] 운동량의 변화량은 운동량과 힘의 관계식을 변형하여 다음과 같이 작성할 수 있다.
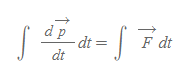
[2] 힘이 일정하고 시간간격이 Δt로 정해진다면 미소 운동량 Δp로 고쳐 쓸 수 있다.
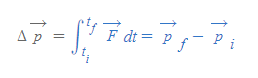
[3] [과정 2]에서 운동량의 변화량을 충격량(impulse) I로 새로 정의한다.
충격량
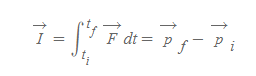
■
- 의미: 충격량은 I로 적고, 특정 시간 간격에 한 입자에 작용한 알짜힘을 곱한 값 또는 운동량의 변화량이다.
- 방향: 운동량의 변화량 방향 Δ(벡터 p)와 일치
- 차원: 운동량과 같은 차원으로 단위 또한 운동량과 같다.
- 외적으로는 외력이 입자의 운동량을 변화시키는 정도로 나타난다. 즉, 충격량이 클수록 입자의 운동량은 크게 변화한다. 그리고 그 충격량의 크기는 (1)강한 외력과 (2)오랜 외력 작용 시간으로 결정된다.
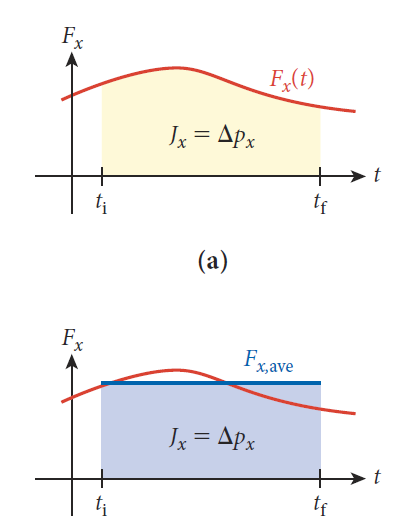
종종 충격량은 기호 J로도 쓰이며, 외력-시간 그래프에서는 면적[그림 2]으로 나타난다.
충격량-운동량 정리 | Impulse-momentum Theorem for a Particle
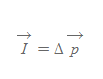
■
- 의미: 입자의 운동량의 변화는 입자에 작용하는 알짜힘의 충격량과 같다.
- 충격량이 입자에 가해짐은, 외부인자에 의해 그 입자에 운동량이 전달된 것으로 해석 가능하다.
- 뉴턴의 운동 제2법칙과 동등한 의미
- 힘-시간 그래프에서 곡선 아래의 넓이는 (1)충격량 또는 (2)운동량의 변화량과 같다.