[물리학-고전역학] 44. 회전운동에너지와 관성모멘트 | Rotational Kinetic Energy and Moment of Inertia

[고전역학_42. 회전운동식과 병진운동식]에서 등가속도 운동식과 등각가속도 운동식의 대응 물리량을 아래와 같이 정리하였다.
[물리학-고전역학] 42. 회전 운동식과 병진 운동식 | The Relationship between Rotational Motion and Transitional
[고전역학_22. 물체의 운동]에서 배운 것과 같이 속도의 변화량이 일정한 운동을 등가속도 운동이라 하듯, ...
blog.naver.com
- 위치 x ↔ 각도 θ
- 속도 v ↔ 각가속도 ω
- 가속도 a ↔ 각가속도 α
지금부터는 [고전역학_08. 뉴턴의 운동법칙]의 내용을 강체의 회전운동 분석에 확장해보자.
- 직선 또는 평면에서 물체는 힘에 의해 가속도를 갖는다. 같은 원리도 강체에서 회전축에 대해 '토크'를 주면 '각가속도'를 얻는다.
- 물체의 가속도는 그 물체에 작용하는 알짜힘에 비례한다. 마찬가지로 강체의 각가속도는 그 강체에 작용하는 알짜토크에 비례한다.
- 토크에 의해 각가속도의 방향과 크기가 결정된다.

위의 비례식은 뉴턴의 운동법칙 중 가속도의 법칙과 매우 유사하다.
회전운동에너지
Rotational Kinetic Energy
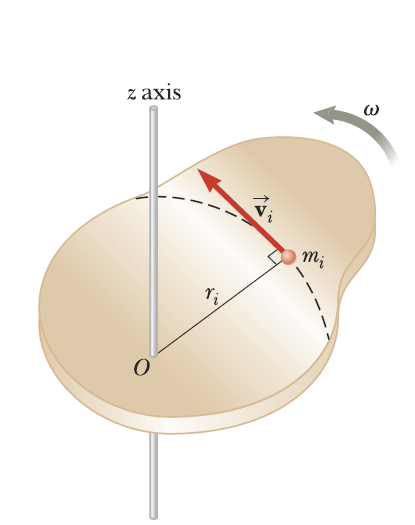
회전축을 따라 고정된 회전운동을 하는 강체의 미시입자는 접선속력을 가짐으로써 회전운동과 관련된 운동에너지를 가질 수 있다.
- 일반적인 물체의 운동에너지 식에서 속력이란, 접선속력을 의미한다.
- 호의 길이공식을 대입한 접선 속력 v = rω이고, 이를 적용한 강체의 미시입자 i가 갖는 회전운동에너지는 다음과 같이 정의할 수 있다.

- 접선속력의 변형식에서 각속력은 모든 입자가 같은 각속력을 가지기 때문에 아래첨자를 붙이지 않았다.
- 다음과 같은 미시입자들이 모두 모인 회전강체 전체의 회전운동에너지는 각 미시입자의 회전운동에너지의 합이다.

- 전체 회전운동에너지 K_R 식에서 괄호 안의 양은 강체의 관성모멘트(moment of inertia)로 정의한다.
관성모멘트 | Moment of Inertia

■
- 정의: 회전운동에 변화를 줄 때 강체가 저항하는 정도
- 질량크기와 함께 회전축 주위로부터의 질량 분포가 관성모멘트 크기에 영향을 준다.
- 단위: kg·m^2
강체의 관성모멘트는 회전운동의 '지속성' 또는 '변화에 대한 저항'을 나타내는 물체의 성질이다. 특히, 회전운동의 상태를 변화시키고자 할 때, 이에 반응(저항)하는 정량적 척도로 활용된다.
관성모멘트의 정의를 활용하면 강체의 회전 운동에너지를 다음과 같이 새롭게 정의할 수 있다.
강체의 회전운동에너지 | Rotational Kinetic Energy

■
강체를 이루는 입자들의 각각의 운동에너지의 합으로 회전운동에너지를 유도하였다.
- I는 병진운동에서의 질량 m과 대응된다.
- ω는 병진운동에서의 속력 v와 대응된다.
관성모멘트를 계산하는 방법만 알면 강체의 회전운동에너지는 매우 쉽게 구할 수 있다.
관성모멘트 계산
Calculations of Moment of Inertia
연속적 입자계: 어떤 강체가 연속적일 때 관성모멘트의 계산은, 각각의 질량이 Δm_i인 수많은 작은 요소들이 이루어졌다고 가정할 수 있고, 이를 적분하여 구할 수 있다.
연속적 입자계의 관성모멘트

■
- 일반적으로는 강체의 경우, 질량 요소보다는 부피요소를 사용하는 것이 계산이 쉬운데, 때문에 연속적 입자계의 식은 다음과 같이 변형된다.

- 일반적으로 강체의 밀도 ρ는 어디서나 일정하다고 본다. 즉, 질량은 밀도×부피로 구할 수 있고, 강체의 경우 밀도가 일정하기 때문에 적분 계산 시 상수항으로 취급할 수 있다.
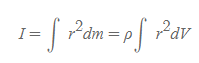
위의 식은 관성모멘트의 적분식으로 고리, 원기둥, 구 등 규칙적인 모양을 가진 강체의 관성모멘트 계산[그림 2]에 활용된다.

그림 2. 다양한 모양의 강체 관성모멘트 [출처: Sears & Zemansky's University Physics with Modern Physics, Young & Freedman, 14th ed., 2016, p.310]