[물리학-고전역학] 47. 벡터 미적분학: 그래디언트(기울기) | Gradient

고전역학에서 다루는 많은 물리량은 벡터량으로 분류되고, 많은 공식은 벡터함수의 꼴을 갖는다. 벡터 미적분학(vector calculus)은 2차원 이상의 벡터의 다변수 실해석(실수집합을 다루는 해석학의 한 분야)과 관련한 미적분학의 한 분야로 벡터장 모델을 구현 및 해석하는 데 필수적이다.
- 장(마당, field): 3차원 공간계를 예로 들면, 어떤 함수 중에서 독립변수가 공간의 위치인 좌표 x, y, z를 가지는 함수를 field라고 정의한다.
스칼라장과 벡터장
Scalar Field and Vector Field
스칼라장
스칼라장(scalar field): 특정한 공간 속의 각 점에 대해 스칼라량을 대응시킨 공간장, 예를 들어 온도 분포가 존재하는 방을 생각할 때 특정 지점에서의 온도 T는 명백히 위치에 따른 함수임을 알 수 있다.
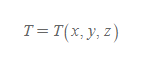
각 지점에 대한 온도 스칼라를 x, y, z로 대응했다.
일반적인 스칼라장은 φ로 적으며, 각 지점에 대해 숫자가 대응되는 공간장을 아래와 같이 표현한다.
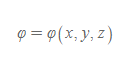
물리학에서 스칼라장은 대표적으로 온도 분포, 수압 분포, 공간 상 전위의 분포, 퍼텐셜 에너지 분포 등이 있다.
스칼라장에서 각 점은 그래디언트(gradient)를 갖는데, 이는 그 지점에서의 힘의 크기 및 방향을 나타낸다.
벡터장
벡터장(vector field): 특정한 공간 속의 각 점에 대해 벡터량을 대응시킨 공간장
- 스칼라장의 공간 위치가 스칼라량이라면, 벡터장의 공간 위치는 벡터량이다. ⇒ 스칼라량 공간위치는 x, y, z-축의 좌표 값인 반면, 벡터량 공간위치는 '위치벡터'를 들 수 있다.
벡터장은 v로 일반적으로 적으며, 벡터장 함수는 아래와 같이 표현한다.
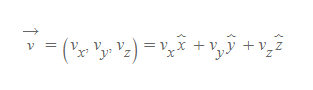
- x hat, y hat, z hat은 벡터에서 배운 단위벡터를 의미하고, 각각은 x-, y-, z-축을 나타낸다.
- 벡터공간의 각 점에 위의 벡터가 대응된다.
- 복소평면에서의 2차원 벡터장 또한 표현이 가능하다.
- 벡터장의 대표적인 예로는 중력장과 전기장, 그리고 자기장 등을 들 수 있다.
그래디언트(기울기)
Gradient
앞서 잠깐 설명하였듯, 그래디언트는 벡터 미적분학에서 스칼라장의 최대 증가율을 나타내는 벡터장[그림 1]을 의미한다.
- 예를 들어 온도장의 그래디언트란, 온도의 증가율이 가장 큰 방향을 가리키는 벡터이다.
- 그래디언트를 나타내는 벡터장을 화살표로 표시할 때, (1)방향은 증가율이 최대가 되는 쪽이며, (2)크기는 증가율의 크기를 뜻한다.
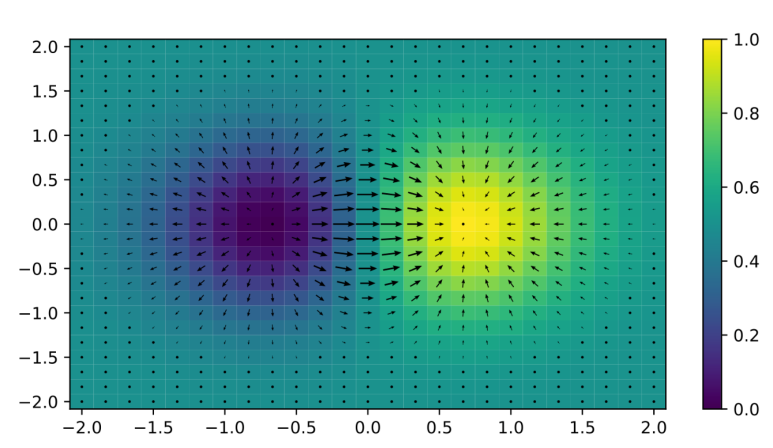
예를 들어 온도장과 같은 스칼라 함수 φ=φ(x, y, z)가 주어질 때, 각각의 독립변수에 대해 편미분하여 아래 항들을 구할 수 있다.
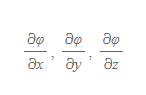
편미분으로 구한 값이 들어간 아래의 벡터는 물리적으로 매우 중요한 의미를 가지는데, 이 벡터 식을 스칼라장 φ의 그래디언트(gradient)이라고 한다.
그래디언트 | Gradient
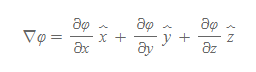
■
- gradient 식의 ∇는 델(del) 또는 나블라(nabla)라고 하며, 이는 연산자로 아래와 같은 의미이다.
델 | Del
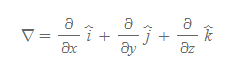
■
- 독립변수가 x, y, z인 스칼라장 함수의 도함수를 구하고 이를 벡터화하는 연산자(operator)
- 스칼라장에 del 연산자를 적용한 결과는 벡터장이다.
위의 풀어쓴 식 대신 간단하게 그래디언트는 grad φ라 하고, 델은 del이라고 쓸 수 있다.
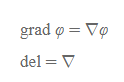
그래디언트의 활용
gradient는 고전역학에서 대표적으로 (1)퍼텐셜에너지의 힘을 구하거나 (2)스칼라퍼텐셜의 장을 구하는 데 활용된다.
먼저 퍼텐셜에너지 V의 힘은 아래와 같이 구한다.
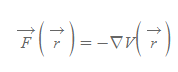
다음 스칼라퍼텐셜 φ의 장은 아래와 같이 구한다.
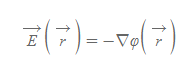
gradient는 스칼라장의 최대 증가율을 나타내는 값으로, 스칼라의 기울기를 표현한다. 그리고 del 연산자(단위벡터 포함)에 의해 gradient는 벡터(량)의 결과 값을 갖는다.