[물리학-고전역학] 48. 벡터 미적분학: 다이버전스(발산) | Divergence

다이버전스(발산, divergence): 벡터 미적분학에 등장하는 벡터 연산자 중 하나로, 계의 한 지점에서 벡터장이 퍼지는 지(발산) 아니면 모여서 사라지는 지(수렴)를 보여준다.
- divergence는 임의의 한 점(x, y, z)이 있는 공간 내에 벡터장이 퍼지는 지 아니면 모여서 사라지는 지를 나타낸다.
- 벡터장의 발산은 각 점에서의 스칼라 값으로 나타난다.
다이버전스 | Divergence

■
- 의미: 델과 벡터장을 '스칼라곱'한 연산자
- 두 벡터의 스칼라곱이 스칼라량인 것처럼 다이버전스도 스칼라량이다. ⇒ divergence는 델 연산자와 벡터장의 내적으로 스칼라장이다.
- 다이버전스를 구하는 연산은 항상 벡터에 대해서만 작용한다. ⇒ divergence는 벡터장에만 사용할 수 있다.
만약 벡터 F=<P, Q>라면, P_x, Q_y는 둘 다 존재하고, div 벡터 F는 아래와 같이 정의한다.

발산의 모양

주어진 한 지점에서 밖으로 나가는 벡터장의 선속이 많은 경우, divergence는 양의 값을 갖는다[그림 1]. 한편 주어진 지점으로 들어오는 벡터장 선속이 많은 경우, divergence는 음의 값을 갖는다.
- 발산의 결과가 양수이면, 한 지점에서 스칼라는 발산한다.
- 발산의 결과가 음수이면, 한 지점에서 스칼라는 소멸(sink)한다.
- 발산의 결과가 0이면, 한 지점에서 스칼라의 변화는 없으며, 이는 곧 장을 변화시키는 원천(source)이 없다는 뜻이다.

또한 발산은 벡터장 자체의 크기가 아닌, 벡터장 크기의 '변화량'을 나타내는 척도임에 유의한다. 예를 들어 div가 양수인 경우, 벡터장의 변화량은 [그림 2]와 같이 표현될 것이다.

한편 발산의 결과 값이 0인 경우는 [그림 3]과 같이 벡터장의 변화량이 표현될 것이다. [그림 3]을 보면 벡터들이 한쪽 방향으로 발산'하는 것처럼' 보이나 상호 인접한 벡터함수 간의 변화량이 없으므로, divergence의 연산 결과가 0으로 계산되었음을 유추할 수 있다.

예를 들어 F=<1, 2>이면, 그래프는 [그림 4]와 같이 그릴 수 있고, div F는 0으로 계산된다. 벡터들은 오른쪽 상단으로 향해 발산'하는 것처럼' 보이나, 상호 인접한 벡터함수 간의 변화량이 없으므로 div F가 0임을 유추할 수 있다.

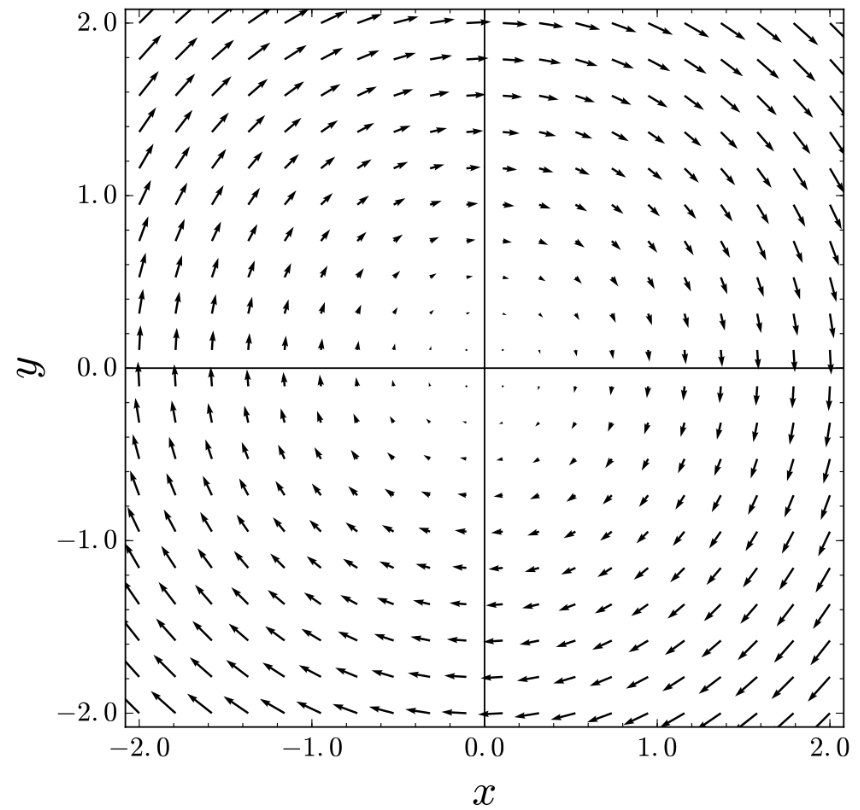
또 다른 예로 F=<-y, x>일 때, div F는 0으로 계산되는데 그래프는 [그림 5]와 같이 그려짐에 주목한다.
솔레노이달
벡터장 중 하나로 유체의 속도장을 들자면, 벡터 F의 다이버전스는 그 점으로부터 나오는 유체의 유출량(output)이나 혹은 그 점을 향해 들어가는 유체의 유입량(input)을 나타낸다.
- 만약 유체의 다이버전스가 모든 곳에서 0이라면, 임의의 점으로부터 유출은 반드시 같은 양의 유입에 의해 상쇄되어야만 한다. 이와 같은 특징을 지닌 벡터장을 특별히 솔레노이달(solenoidal)이라 부른다.
- solenoidal 벡터장(solenoidal vector field)[그림 6]은 (1)알짜 source는 없는 결과 또는 (2)한 지점에서 sink하는 특성을 갖는다.
발산의 응용
특정 지점에서의 벡터장 흐름 판단
솔레노이달 설명에서 다이버전스는 그 지점으로부터 유체의 '유출량' 또는 '유입량'로 설명했다. 예를 들어 아래와 같은 유체속도 벡터장 F를 떠올려보자.
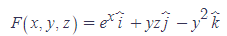
이때 (0, 2, -1) 지점에서의 벡터 F의 divergence를 계산해보자.
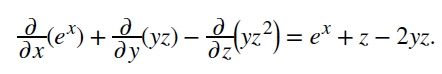
divergence의 계산 결과인 e^x+z-2yz에 (x=0, y=2, z=-1)을 대입한다.

divergence의 결과는 양수 스칼라량 4로 계산되었고, 이는 벡터장 (0, 2, -1) 지점에서 유출량(flowing out)이 더 많음을 의미한다.
다이버전스 테스트 | Divergence Test for Source-Free Vector Fields
만약 어떤 벡터장 F(x, y)가 아래와 같이 주어졌을 때, div F를 계산하여 그 벡터장이 장을 변화시키는 원천(source)으로 부터 자유로운 지를 판단할 수 있다.
- div 벡터 v = 0이면, 벡터장을 변화시키는 원천으로부터 자유롭다.
- div 벡터 v ≠ 0이면, 그 벡터장 내부에 장을 변화시키는 원천이 있다.