【미분적분학 2】 Chapter 8. 삼각함수적분

적분의 대표적인 전략으로 지금까지 IBS(치환적분법)과 IBP(부분적분법)를 알아보았다. 하지만 이 전략들 이외에도 피적분함수의 형태에 따라 몇 가지 적분법이 더 있다.

 

1. 삼각함수적분(Integrals of Trigonometric Functions, ITF)

2. 부분분수적분(Integration by Partial Fraction Decomposition, IPFD)

3. 삼각치환적분(Integration by Trigonometric Substitution, ITS)

 

삼각함수 적분을 위해서는 삼각함수 항등식을 반드시 복습해야 한다.

​

 

삼각함수 적분은 피적분함수의 삼각함수 형태에 따라 다음과 같이 정리할 수 있다.

 

 

삼각함수의 반각공식은 삼각함수의 배각공식으로부터 유도할 수 있고, 두 식은 다음과 같이 정리할 수 있다.

 

 

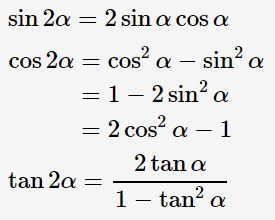
배각공식

 

 

반각공식

 

 

6가지의 삼각함수 적분 응용 이외에도, 경우에 따라 탄젠트 함수의 적분과 시컨트 함수의 적분도 필요하다.

 

탄젠트 함수의 적분

 

■

 

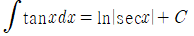
연쇄법칙을 공식화한 스코틀랜드의 수학자 그레고리가 시컨트 함수의 적분식을 고안했다.

 

 

James Gregory (1638~1675, 스코틀랜드)

 

시컨트 함수의 적분

 

■