【물리학 - 고전역학】 04. 위치, 속력, 속도

물리학에서 가장 먼저 다루는 내용은 운동학(kinematics)으로 변화하는 세계의 움직이는 물체를 표현하고, 이 물체가 앞으로 어떻게 움직일 지를 예측하는 데 매우 큰 도움이 된다. 운동을 이해하기 위해 먼저 시간과 공간의 개념을 활용해 운동을 기술하는 법을 익힌다.
- 운동학은 운동 기하학이라고도 불린다. (Russell, 2009)
- 운동학이란, 물체에 가해진 힘(force)을 고려하지 않은 채, 점, 부피, 계(systems of bodies) 형태를 포함한 모든 물체의 움직임을 기술하는 고전역학의 한 분야이다. (Whittaker, 1904)
고전역학의 세부분야는 크게 두 가지로 나뉜다.
- 운동학(kinematics): 물체의 운동을 기술하는 고전역학의 세부분야
- 동역학(dynamics): 물체의 운동을 야기하는 힘의 요소를 다루는 고전역학의 세부분야
- 동역학은 물체의 종류에 따라 강체동역학, 유체동역학, 연체동역학 등으로 나뉜다.
위치, 이동거리, 변위
Position, Distance Travelled, and Displacement
입자모형(particle model): 물리학에서 입자란, 더 이상 물리적인 변형을 가할 수 없다고 가정한 물체를 뜻한다. 특히 점과 같은 입자는 질량만 존재할 뿐 크기와 부피는 존재하지 않는다고 생각한다.
위치
입자의 위치(position) x는 좌표계에서 원점이라 생각해 선택한 기준점에 대한 입자의 위치를 뜻한다.
- 절대위치(absolute location): 좌표계에서 특정한 고도와 경도 쌍을 사용해 지정된 지점
- 상대위치(relative location): 어떤 다른 지점으로부터 떨어진 정도를 나타내는 지점
물체는 어떠한 위치로부터 다른 위치로 '이동'이 가능하며 이로 인해 이동거리와 변위가 발생한다.

변위(displacement, Δx): 어떤 물체의 위치변화
변위

■
- 변위란, 어떤 물체 또는 입자의 최종 위치에서 초기 위치를 뺀 값이다. [그림 1]과 같이 이동할 경우, 3.5-1.5=+2.0[m]로 계산되는데, 여기서 (+)는 일반적으로 물체가 오른쪽으로 간 것으로 해석한다.
- Δ는 변화량으로 물리량 앞에 델타 기호는 그 물리량의 종류와는 상관없이 최종값에서 초기값을 빼라는 의미이다.
변위는 다음과 같은 특징을 가진다.
- 변위는 물체의 이동방향을 고려해야하는 벡터량이다.
- 벡터량으로서 변위의 부호는 다음과 같이 해석한다.
- Δx>0 = 오른쪽으로 움직이는 물체, (+)
- Δx<0 = 왼쪽으로 움직이는 물체, (-)
- 변위의 공식에서 알 수 있듯이, 입자의 초기위치와 최종위치 값에만 관심이 있다.
<이동방향>
변위는 물체의 이동방향을 고려한다. 반면 이동거리(distance travelled, d)는 물체의 움직인 양 그 자체에 관심을 가지므로 움직임 경로와 상관없이 이동한 총 길이를 의미한다.
- 이동거리는 변위와 달리 스칼라량이다.
- 입자가 이동한 총 이동거리는 변위보다 항상 크거나 같다[그림 2].


|
스칼라량과 벡터량
스칼라(scalar): 물리학에서 스칼라란, 크기로 규정되는 물리량이다.
벡터(vector): 물리학에서 벡터란, 크기와 함께 방향도 함께 고려해야 하는 물리량이다.
|
속도와 속력
Velocity and Speed
변위와 이동거리에 대해 시간 간격으로 나누면, 각각 속도와 속력이 유도된다.
- 속도(velocity): 변위를 변위가 일어난 시간 간격으로 나눈 값
- 속력(speed): 이동거리를 이동거리가 발생한 시간 간격으로 나눈 값
속도

■
속력

■
특히, 위의 속도 식을 활용하면 물체의 속도가 일정할 경우(등속 운동) 입자의 최종 위치를 구할 수 있는 식을 유도할 수 있다.

등속 운동을 하는 입자의 최종 위치
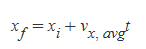
■
속도와 속력의 단위는 변위와 시간의 표준 단위를 조합한 [m/s]이다.