[대학수학 - 미분적분학] 06. 극한의 부정형 계산과 로피탈의 정리 (예제 포함)

0/0 부정형
f(x)와 g(x)가 다음과 같다고 하자.
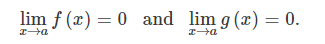
식 1
f(x)/g(x)는 식 1의 조건에 따라 x=a에서 0/0의 부정형 꼴을 갖는다.
x-a 지점에서 0/0 부정형의 함수 f(x)/g(x)의 극한을 구하기 위해서는 먼저 분자와 분모를 인수분해(factor)한 뒤, 0으로 접근하는 항을 소거(reduce)하도록 한다.
EXAMPLE.
다음 식을 구하시오.

식 2
SOLUTION.
식 2에 1을 대입하면 0/0 꼴의 부정형 극한이 나온다.

분자를 인수분해하여 0으로 접근하는 항을 소거하자.

답은 2이다.
■
∞/∞ 부정형

여기서 a는 실수, 또는 +∞, 또는 -∞이다.
따라서 f(x)/g(x)는 x=a에서 ∞/∞의 부정형 꼴을 갖는다.
∞/∞ 부정형의 함수 f(x)/g(x)의 극한을 구하기 위해서는, f(x)/g(x)의 분모 항에 존재하는 가장 높은 지수의 x(the highest power of the fraction)를 찾아 분자와 분모 모두에 이 값을 나눔으로써 구할 수 있다. 자세한 계산 과정은 예제를 통해 확인하자.
EXAMPLE.

식 3
SOLUTION.
f(x)/g(x)[식 3]에 존재할 수 있는 가장 높은 분모의 차수의 x는 x^30이다.

■
로피탈의 정리
L'Hopital's Rule

Guillaume de l'H ô pital (1661~1704, 프랑스)
요한 베르누이의 제자이자 프랑스의 수학자 로피탈(Guillaume de l'Hôpital, 1661~1704)은 '재정적 도움'을 조건으로 베르누이가 발견한 아이디어를 자신에게 팔 것을 요구했다. 베르누이의 승낙 후, 로피탈은 자신의 저서 『Analyse des Infiniment Petits pour l'Intelligence des Lignes Courbes』(1696)에 이 내용을 실었는데, 이것이 훗날 로피탈의 정리로 불린다.
로피탈의 정리

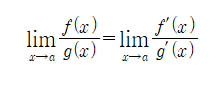
식 4
단, f, g가 a 근방에서 미분가능하고, g'(x)≠0이다.
■
PROOF. 로피탈의 정리
로피탈 정리의 증명은 식 4가 성립하는 지를 확인하면 된다.

■
로피탈 정리의 유의점
1. 로피탈 정리를 사용하기 전, f와 g의 극한에 대한 조건을 반드시 확인하자.
2. 로피탈 정리를 사용할 때, 분모와 분자는 각각 따로 미분해야 한다. 몫의 법칙은 사용하지 않는다.
3. 로피탈 정리는 일방향의 극한 뿐만 아니라 무한이나 음의 무한 극한에 대해서도 성립한다.
EXAMPLE.
다음 식을 구하시오.

SOLUTION.
f(x)와 g(x)는 각각 lnx, x-1이다.
[1] f' 구하기
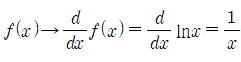
[2] g' 구하기

[3] 식 4 활용

■

극한의 부정형으로 지금까지 0/0 부정형, 그리고 ∞/∞ 부정형을 알아보았다. 이외에도 실전문제에서는 다음과 같은 부정형도 만날 수 있다.
- 차 부정형: ∞-∞ 부정형
- 곱 부정형: 0×∞ 부정형
차 부정형의 풀이

식 5
차 부정형은 식 5의 형태로 무한대를 그대로 대입하면 연산 결과가 0 또는 무한대로 구해진다. 차 부정형은 식의 종류에 따라 다음 풀이법을 갖는다.
1. 식이 다항식-다항식 꼴이라면, 먼저 최고차항을 묶어주어 계산한다.

식 6
식 6은 최고차항이 x^2이므로, 이를 묶어주면 다음과 같이 계산할 수 있다.

2. 식에 무리식이 있다면, 유리화를 해준다.

식 7
식 7에 존재하는 무리식을 다음과 같이 풀어 계산할 수 있다.

EXAMPLE.
다음 식을 구하시오.

SOLUTION.

■
곱 부정형의 풀이
무한소 0의 정의

따라서, ∞/∞는 아래와 같은 이유로 무한소 0/무한소 0임을 알 수 있다.

0×∞ 부정형과 0/0 부정형은 서로 같은 특징을 공유한다.
- 두 부정형의 0은 숫자 0이 아닌 무한소 0을 의미한다.
- 무한소 0은 수가 0을 향해 줄어드는 상태를 의미한다.
EXAMPLE.
다음 식을 구하시오.

식 8
SOLUTION.
식 8에 ∞를 그대로 대입하면 0×∞ 부정형으로 볼 수 있다.

■
차수대조법

식 9
식 9와 같은 식을 푼다고 하자. 식 9는 ∞/∞ 부정형으로 분모의 최고차항 x로 분자와 분모를 나누어 극한 값을 구할 수 있다.

식 10
식 10의 풀이를 위해 유리수의 무한대 극한 성질을 활용했다.
유리수의 무한대 극한

■
식 10의 풀이 과정은, 극한을 계산할 때 분자와 분모의 차수가 같다면 분자와 분모의 최고차항의 계수만 고려하면 됨을 알려준다.
차수대조법
- 분자와 분모의 차수가 같다면 분자와 분모의 최고차항의 계수만 고려한다.
- 분자의 차수가 분모의 차수보다 크면 ∞ 또는 -∞이다.
- 분모의 차수가 분자의 차수보다 크면 0이다.
■

식 11
식 11은 분자와 분모의 최고차항이 서로 같기 때문에 분모의 최고차항을 나눌 것 없이 바로 최고차항의 계수만으로 답을 구하면 된다.
EXAMPLE.
다음 식을 구하시오.

SOLUTION.

■