[대학수학 - 미분적분학] 08. 곱미분과 몫미분

곱미분
Product Rule(PR)
함수 f와 g(이전 함수, 구함수)가 모두 미분 가능할 때, 이전 함수를 곱하거나 나눔으로써 얻어지는 새로운 함수의 도함수 역시 구할 수 있다.
- 곱미분은 구함수를 곱하여 얻은 새로운 함수의 도함수를 구하는 방법을 의미한다.
곱미분 Product Rule - PR
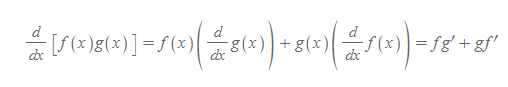
■
- 두 함수의 곱의 도함수는 앞의 함수에 뒤의 함수의 도함수를 곱한 값에 뒤의 함수에 앞의 함수의 도함수를 곱한 둘을 더한 값과 같다.
만약 세 함수 f, g, h를 곱한 것을 구한다고 하면 곱미분은 다음과 같이 확장될 수 있다.
확장된 곱미분

■
곱미분의 증명
[1] f(x)와 g(x)는 미분가능한 함수이고, 만약 r=f(x)g(x)라 하면,
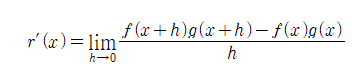
이다.
[2] 여기서 분자 항에 f(x)g(x+h)를 각각 더 하고 빼 보자.
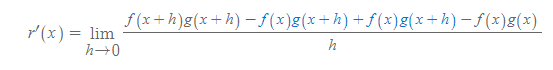
[3] 위의 극한에서 분자 항에 추가된 항의 합산은 마찬가지로 0이다. 이제 이를 극한 법칙을 이용해 아래와 같이 분해해보자.
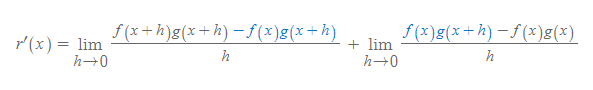
[4] [과정 3]의 결과를 아래와 같이 재정리한다.
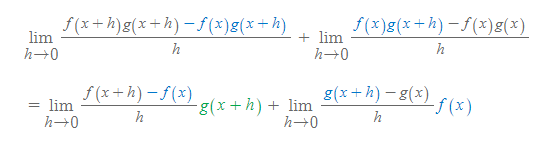
- [과정 3]의 결과에서 공통인자가 초록색 항으로 나타난다.
[5] g(x)는 연속하므로,
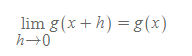
가 성립한다. 그리고 이를 [과정 4]에 적용하면 아래와 같다.
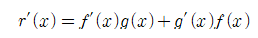
□

일반적으로 곱미분은 라이프니츠를 발견자로 인정하고 있다. 그러나 라이프니츠의 저작물을 번역한 J. M. Child과 같은 학자들은 발견자로 뉴턴의 스승 아이작 배로(Isaac Barrow, 1630~1677)를 지목하기도 한다.
몫미분
Quotient Rule(QR)
PR은 구함수의 곱에 대한 도함수의 계산법이라면, 몫미분(quotient rule - QR)은 두 함수를 나누어 얻은 새로운 함수의 도함수를 구하는 방법을 뜻한다.
몫미분 Quotient Rule - QR
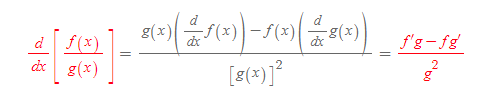
■
몫미분의 증명
[1] 함수 F(x)가
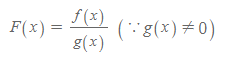
일 때, 양변에 g(x)를 곱하면,

이다.
[2] PR을 이용하면,
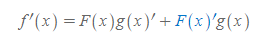
로 계산된다.
[3] [과정 2]의 PR의 결과 속에 F(x)의 미분항이 들어있는데 이것이 바로 우리가 증명하려는 몫미분의 내용과 같다.