[물리학-고전역학] 선적분 | Line Integral

선적분(line integral): 곡선적분, 평면 위의 곡선을 따르는 함수의 적분
직선 위의 정적분을 곡선 위의 적분까지 일반화한 개념으로 물리학에서는 장의 종류에 따라 (1)스칼라장 선적분과 (2)벡터장 선적분으로 구분된다.
- 스칼라장 선적분: 밀도의 분포가 주어진 끈의 질량을 구하는 문제와 동일
- 벡터장 선적분: 어떤 주어진 벡터장에서 경로를 따라 운동하는 물체에 한 일을 구하는 문제와 동일
- 벡터장을 물체의 운동경로에 따라 선적분하면, 힘이 물체에 한 일을 구할 수 있는데, 이때 힘이 한 일이 출발점과 도착점의 위치에만 의존하고, 경로와는 무관하다면 그 힘을 '보존력'으로 분류할 수 있다. 그리고 이 보존력장의 원함수를 그 힘에 의한 퍼텐셜에너지로 정의한다.
중력 하에 있는 질량 m의 물체에 대해 중력장은 벡터장으로 작용한다.
- 질량에 가해지는 중력은 (벡터 F)=m(벡터 g)로 계산된다.
중력가속도 g는 고도가 극히 높지 않은 이상 일정한 값의 상수 벡터로 취급한다. 그러므로 중력장 내에 물체를 ds만큼 움직였을 때, 한 일은 아래와 같은 관계식을 가진다.
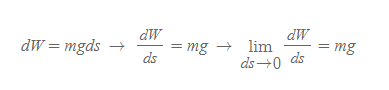
질량이 지점 A에서 B로 낙하할 때, 중력이 한 전체 일은 관심 영역 전반에 걸쳐 기여한 양을 모두 더하거나 혹은 적분해야 한다.
dW/ds=mg 관계식의 양변에 ds를 A에서 B구간까지 구간적분하면,

로 '물체의 낙하 시 중력장이 한 일'을 구할 수 있다.
중력장에서의 운동은 직선의 운동경로 였다. 하지만 곡선 운동경로는 좀 더 많은 요소를 주의 깊게 정의해야 한다.
평면 상에서 곡선경로로 이동하는 물체
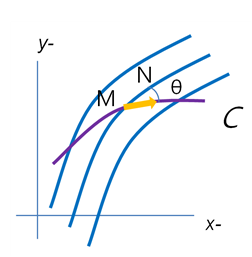
[그림 1]과 같이 평면 상에서 곡선경로 C로 이동하는 물체가 곡선 형태의 벡터장 F(파란색 곡선다발)에 놓였다고 하자. 우선 이동좌표, 적분식 등의 정보는 다음과 같다.
- 이동좌표: (x_1, y_1)에서 (x_2, y_2)
- 적분식
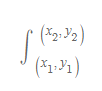
x와 y가 변함에 따라 벡터장 F도 함께 변한다.
벡터 F는 x와 y의 함수이므로, 직각좌표 성분 F_x=P(x, y)와 F_y=Q(x, y)를 가질 것이고 따라서 벡터 F는 다음과 같이 쓸 수 있다.
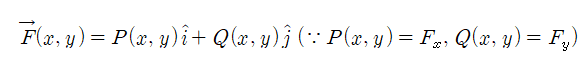
곡선 C에 포함된 작은 요소는 [그림 1]의 M점 N과 을 이어주는 벡터로 표기할 수 있다.
C의 미소부위

위의 그림에서 벡터장은 곡선경로 C와 각 θ를 이루며 교차하고 있는데, 이 각도 성분을 고려하여 벡터함수를 아래와 같이 정리할 수 있다.
- 극도로 작은 크기(ds)를 가진 벡터량을 고려했을 때, 곡선경로와 각성분을 이용해 다음과 같은 관계식을 유추할 수 있다.
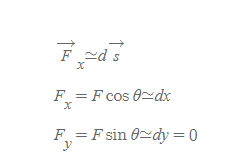
- 곡선경로와 밀접한 벡터필드 성분은 x축 방향이다.
F_x=Fcosθ=dx
선에 관한 미소벡터의 스칼라곱
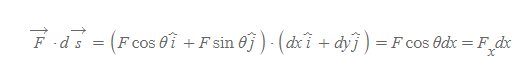
다음 선에 관한 벡터장의 전체 적분을 할 수 있다.
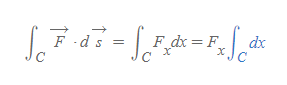
- 여기서 파란색 부분이 전체 선적분을 의미한다.
선적분은 벡터장에서 선 경로를 따라 벡터함수를 '스칼라곱'한 값이다.