[물리학-고전역학] 중력장과 중력선속 | Gravitational Field and Flux

대학 물리학에서 가우스 법칙은 '선속'의 개념으로 인해 전자기학에서 본격적으로 다루지만, 같은 원리를 활용해 어떤 지점에서의 '중력장'과 '중력선속'을 구할 수 있는 일반식(중력장에서의 가우스 법칙)을 유도할 수 있다. [전자기학_전기장 2]와 [전자기학_가우스 법칙]의 내용을 함께 참조하도록 한다.
[물리학-전자기학] 06. 전기장 2 | Electric Field (2)
전기선속 전기선속(전기다발, flux of electric field intensity): 전기력선 다발 또는 집합 전기선속은 어...
blog.naver.com
만유인력으로부터 중력장과 중력장선의 개념 유도
장(field, 場)이란, 어떤 공간에서의 위치, 시간 등에 따라 그 성질을 달리하는 물리량으로, 직관적으로 중력장이란, [그림 1]과 같이 원천 질량(source mass, M)에 의해 '장'이 펼쳐지면서 특정 공간에서의 물리적 성질이 달라지는 공간을 의미한다. 중력장에서 물체 간 상호작용은 만유인력으로, 음의 전하가 자기에게로 수렴하는 방향으로 전기장을 만들었듯이, 질량 또한 자신에게로 수렴하는 방향으로 중력장을 만든다.
- 물체가 가진 질량은 물체 주변 공간을 왜곡시키는 장을 만들고 이는 마치 경사(slope)와 같이 작용한다.
- 임의의 장에 놓인 질량을 시험 질량(test mass, q_0)이라고 한다.
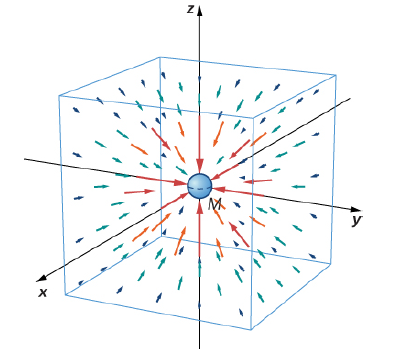
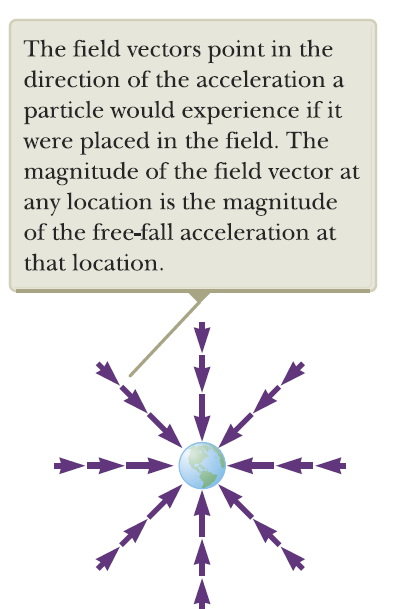
- 중력장은 벡터장으로, 초기 조건이 주어졌을 때, 유클리드 공간의 모든 점에서 단위 질량이 느끼는 힘의 크기와 방향을 구할 수 있다. ⇒ [전자기학_전기장 1] 참고
[물리학-전자기학] 05. 전기장 1 | Electric Field (1)
장 이론 장(field) 정의 1: 공간에서의 위치, 시간 등에 따라 그 성질을 달리하는 물리량 정의 2: 공간의 ...
blog.naver.com
중력장 Gravitational Field
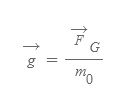
■
- 의미: (원천질량에 의한) 중력장이란, 특정한 시험질량 m_0에 작용하는 중력의 표현이다.
- 방향: 시험질량이 중력장에 놓였을 때 가지는 힘의 방향과 일치한다. ⇒ 중력장의 방향은 항상 원천질량의 중심을 향한다.
- 시험질량 또한 중력장을 형성하지만 중력장의 정의에서는 이 요소는 고려하지 않는다.
- 자기 자신이 만든 중력장이 다시 원천(source)에게 영향을 끼칠 수 없다.
중력장은 만유인력의 법칙으로부터 유도가 가능하다. ⇒ [고전역학_뉴턴의 발견 - 중력의 법칙] 참고
[물리학-고전역학] 07. 뉴턴의 발견 - 중력의 법칙 | Law of Gravity
동역학 동역학(dynamics): 물체 운동에 영향을 주는 원인인 힘(force)과 질량(mass)에 대한 역학의 세부분...
blog.naver.com
- 만유인력의 방향성은 항상 원천질량의 중심을 향하므로, 여기서는 힘의 크기 값을 고려한다.
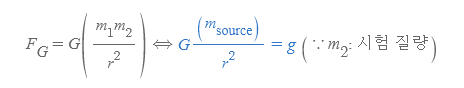
- 물리량
- m_source: 중력장을 만드는 질량(원천 질량), 만유인력의 법칙의 식에서 m_1을 원천 질량으로 간주한다.
- r: 시험 질량과 원천 질량 사이의 거리
- G: 만유인력 상수, 약 6.673×10^-11[N·m2·kg^-2]
- g: 중력장
중력선속
Flux of Gravitational Field Intensity
중력선속: 중력장을 표현하는 선(중력장선)[그림 2]들의 집합 또는 다발
- 중력선속은 어떤 면을 통과하는 중력장선들의 개수에 비례한다.
- 중력선속 내 실질적인 중력장선의 개수를 기호로 Φ_g라 쓴다.
중력선속의 크기
중력선속의 크기는 (1)전기장 연구와 (2)시간 당 부피 흐름률의 개념으로부터 각각 힌트를 얻을 수 있다.
전기장
- 전기장의 크기는 전기력선에 수직한 면의 면적에 대한 전기력선의 개수로 정량적 계산이 가능하고 식은 아래와 같다.
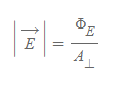
시간 당 부피 흐름률: 면벡터의 도입
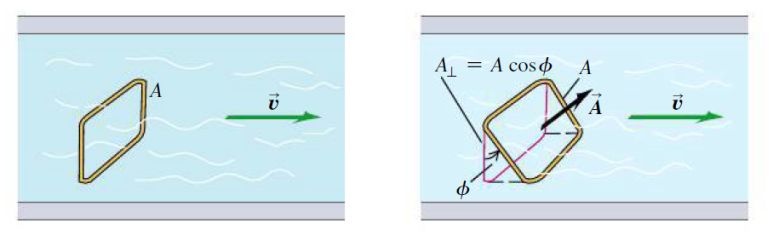
면벡터의 도입은 시간(t) 당 부피(V)의 흐름률과 연관되어 있고, 다음과 같이 식이 정의된다.
시간 당 부피 흐름률 | Volume Flow Rate
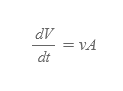
■
- 물리량
- v: 유체 등 흐를 수 있는 것들의 선속(flux)의 속력
- A: [그림 3]의 표면적
- V: 표면적 A를 지난 유체의 전체 부피로 단위는 세제곱미터[㎥]
[그림 3]과 같이 면 A의 표면적에 대해 유체가 속도 v로 흐른다 가정하자. 이때, 둘의 곱은 시간 당 표면적 A를 지난 유체의 부피의 양과 비례한다.
- 그러나 만약 면 A의 표면적에 대해 유체가 각 θ를 가지고 비스듬히 흐르면, 같은 시간 당 총 흐른 부피는 평행할 때 보다 그 양이 적어지게 된다.
비스듬한 각도 θ로 표면적과 유체 흐름이 이루어질 때, 부피 흐름률의 크기는 cosθ의 항을 추가함으로써 표현할 수 있다.
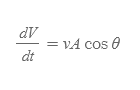
- 만약 θ가 0도로 v와 A가 서로 평행을 이룬다면 cos0=1이므로 dV/dt = vA의 최대값을 만족한다.
- 만약 θ가 90도로 v와 A가 서로 수직을 이룬다면 cos90=0이므로 dV/dt=0, 즉, (시간 당) 부피 흐름률이 없다.
중력장의 flux 역시 유체의 흐름처럼 거동한다 간주하면, 면벡터 등의 개념을 같은 논리로 활용할 수 있다.
중력장 크기
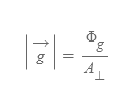
■
- 물리량
- Φ_g: 어떤 질량 m에 의한 중력선속
- A_⊥: 중력장선에 수직한 면의 면적
중력장이 강한 영역에서 중력장선은 높은 밀도를 갖는다. 중력선속은 위의 식으로부터 쉽게 유도 된다.
위의 식은 중력장의 방향과 면이 서로 수직할 때만 성립하는 공식으로 만약 [그림 4]과 같이 각도를 이룬다면, 중력선속의 식은 최종적으로 아래와 같이 바꾸어 쓸 수 있다.

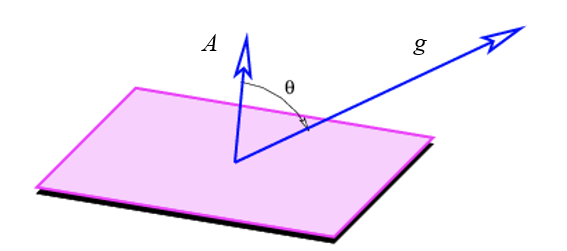
중력선속
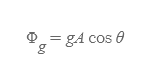
■
중력선속의 크기는 중력장 g와 면에 대한 법선이 일정한 각도 θ에 의해 영향을 받는다.
- θ가 0이라면 cos0 = 1이므로, 그 크기는 gA와 같다.
- θ가 90도라면 cos90 = 0이므로, 그 크기는 0과 같다.