고급물리학/고전역학
[물리학-고전역학] 적용: 중력장에서의 가우스 법칙 | Applications: Gauss's Law for Gravity
herald-lab
2023. 11. 5. 14:23
728x90
반응형

질량 분포에 따른 가우스 법칙
Applications to Mass Distributions
가우스 면의 설정에 따라 가우스의 법칙은 다양한 결과 식을 갖는다.
- 가우스 법칙은 장의 크기가 일정하고 원천 또한 일정한 밀도를 가질 때 적용 가능하다.
- 중력장의 방향과 면 법선의 방향이 평행하는 경우, 중력선속의 스칼라곱은 gA이다. ⇒ cos0=1, 최댓값
- 중력장의 방향과 면 법선의 방향이 수직하는 경우, 중력선속의 스칼라곱은 0이다. ⇒ cos90=0, 최솟값
가우스 법칙으로 표현한 일정한 크기의 중력장
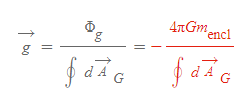
■
구 질량분포
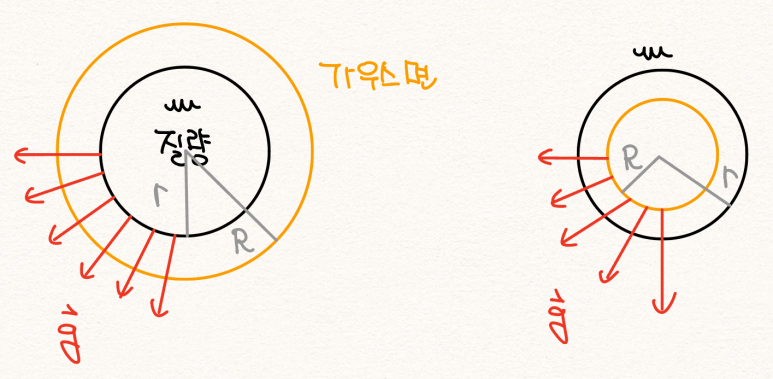
구 질량분포의 중력장을 가우스 법칙으로 계산해보자.
구 외부, 한 점에서의 중력장 크기
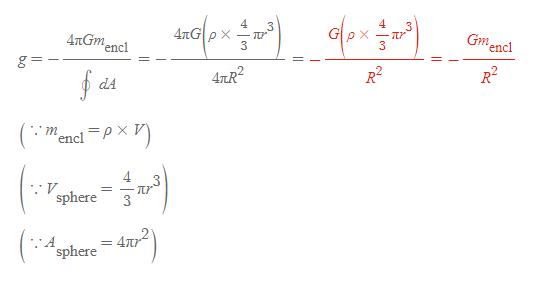
q.e.d
- 물리량
- G: 만유인력 상수
- m_encl: 가우스 표면에 갇힌 원천 질량
- R: 구 형태의 가우스 곡면의 반지름, 반지름의 측정 시작점은 질량중심이다.
구 외부, 한 점에서의 중력장 크기[그림 1]
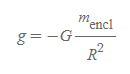
■
한편 구 내부에서의 임의의 한 점에 대한 중력장 크기도 구할 수 있다.
구 내부, 한 점에서의 중력장 크기
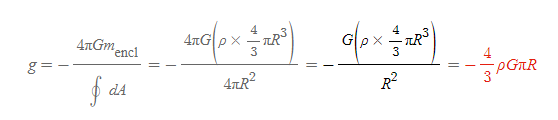
q.e.d.
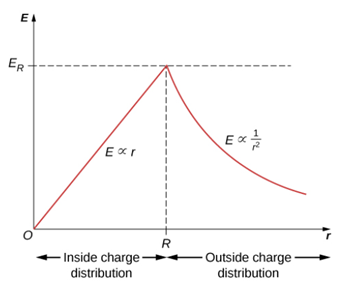
구 내부, 한 점에서의 중력장 크기
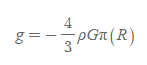
■
- 구 외부의 중력장 크기는 1/R^2에 비례하는 반면 구 내부의 중력장 크기는 가우스 곡면의 반지름 R에 비례한다.
- 부도체 구의 전기장 크기 그래프와 정확히 일치한 그래프[그림 2]를 그릴 수 있다. ⇒ 전기장 E 대신 중력장 g로만 내용을 바꾸면 된다.
즉, 구 대칭 질량분포에 대한 가우스면을 어디에 설정하느냐에 따라, 중력장의 크기는 가우스 면 반지름 R에 비례하거나 혹은 제곱에 반비례할 수도 있다.
- 구 대칭 질량분포 내 가우스 면 반지름에 대해 중력장의 크기는 비례한다.
- 구 대칭 질량분포 외 가우스 면 반지름에 대해 중력장의 크기는 제곱에 반비례한다.
무한 선대칭 질량분포
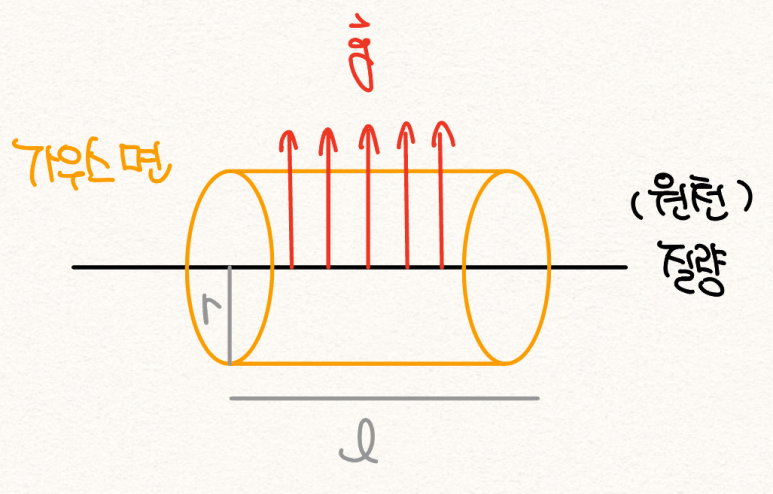
질량이 분포된 선이 무한히 길다고 설정하면, 점의 수직 위치에 상관없이 선으로부터 같은 거리에 있는 모든 점에서 중력장의 크기는 일정하다.
가우스 면은 원통 모양으로 선을 감싼 형태[그림 3]로, 가우스 면에 갇힌 질량은 다음과 같다.
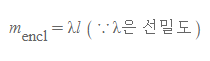
무한 선대칭 중력장 크기
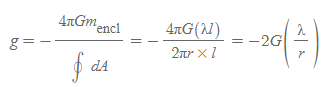
q.e.d.
무한 선대칭 중력장 크기
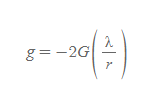
■
- 의미: 선대칭 질량분포의 경우, 중력장의 크기는 선질량 밀도에 비례하고, 떨어진 거리에는 반비례한다.
무한 평면 질량분포
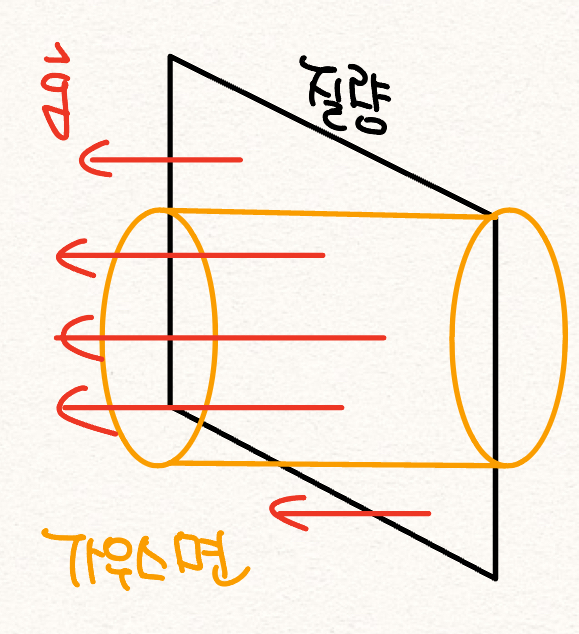
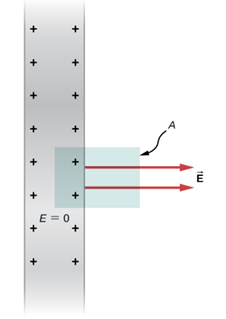
질량를 띤 평면이 무한히 크면[그림 4], 평면으로부터 떨어진 모든 점의 중력장 크기는 같다.
- 중력장은 모든 점에 대해 그 평면의 수직한 방향으로만 방사한다.
- 가우스 면의 설정: 평면에 수직인 축을 가지고 각각의 넓이가 A인 평면을 관통한 원통으로 곡면을 설정한다.
무한 평면 중력장 크기
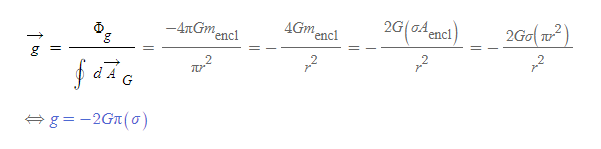
q.e.d.
- 무한평면에 대한 가우스 원통은 2개의 원넓이(πr^2)로 구성되어 있으나 무한 평면의 중력장 크기는 [그림 5]와 같이 가우스 곡면 평면을 '뚫지 않은' 가우스 원통을 가정한다.
무한 평면 중력장 크기
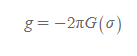
■
728x90
반응형