[물리학-고전역학] 42. 회전 운동식과 병진 운동식 | The Relationship between Rotational Motion and Transitional Motion

 

[고전역학_22. 물체의 운동]에서 배운 것과 같이 속도의 변화량이 일정한 운동을 등가속도 운동이라 하듯, 어떤 물체가 회전 운동 시, 각속도의 변화량이 일정하면, 그 운동을 등각가속도 운동이라 한다.

​

https://blog.naver.com/sortie0228/223186303715

[물리학-고전역학] 22. 물체의 운동 | Motion of Objects

​

일정한 각가속도에서의 강체의 운동: 등각가속도 운동

등각가속도 운동(motion under constant angular acceleration): 고정축을 중심으로 강체가 회전을 할 때, 각가속도가 일정한 경우

• 회전운동에 대한 분석모형으로 등가속도 운동와 같이 각속도의 변화량이 일정한 점을 응용한다. 등가속도 운동(운동학 식)에 사용한 여러 물리량들을 강체의 회전운동에 대응할 수 있다.

1. 위치 x ↔ 각도 θ
2. 속도 v ↔ 각가속도 ω
3. 가속도 a ↔ 각가속도 α

​

먼저, x축에서 등가속도 운동(운동학 식)은 다음과 같다.

 

​

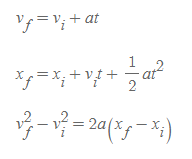
다음 서로 대응이 가능한 물리량으로 치환해 회전 운동식(rotational kinematic equations)을 아래와 같이 세울 수 있다.

​

회전 운동식 | Rotational Kinematic Equations​

■

회전 운동식은 각가속도 α가 일정할 때만 사용할 수 있는 식이다.

​

회전 운동식 그래프

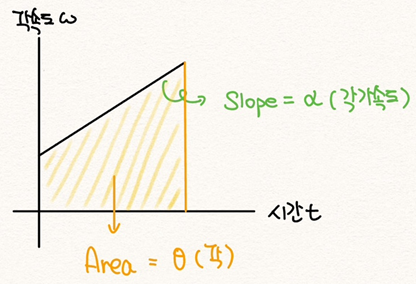
등가속도 운동에서의 v-t 그래프를 분석할 때, (1)기울기와 (2)면적이 각각 가속도와 변위를 나타낸 것처럼 등각가속도 운동에서의 ω-t그래프를 [그림 1]과 같이 정리할 수 있다.

 

그림 1. ω-t 그래프

 

 

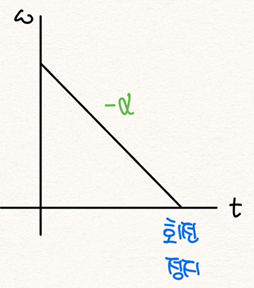
벡터량으로서 각속도와 각가속도의 일치성에 따라 강체의 회전이 빨라지거나 느려짐을 배웠다.

1. 각가속도와 각속도의 방향이 서로 같으면 강체의 회전이 빨라진다.
2. 각가속도와 각속도의 방향이 서로 다르면 강체의 회전이 느려진다[그림 2].

 

 

그림 2. 강체의 회전이 정지할 때 ω-t 그래프

 

 

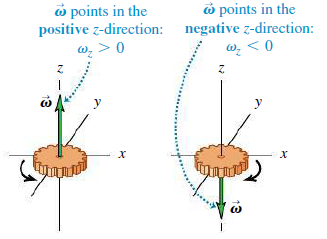
각속도의 방향은 회전이 시계방향이면 z축을 기준으로 (+)로, 반시계방향이면 z축을 기준으로 (-)라 정의[그림 3]했다.

 

그림 3. 각속도의 방향 [출처: Sears & Zemansky's University Physics with Modern Physics, Young & Freedman, 14th ed., 2016, p.300]

 

회전운동식과 병진운동식의 관계

 

그림 4

 

 

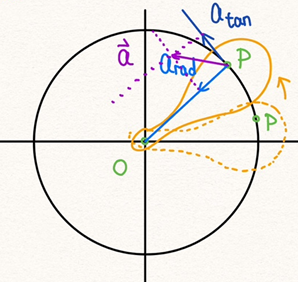
[그림 4]와 같이 주황색의 강체가 회전할 때 한 점 P에서의 병진 가속도 및 구심 가속도 사이의 관계를 알아보자.

• 강체가 고정축을 중심으로 회전할 때, 강체의 모든 입자들이 회전축을 중심으로 원운동을 한다.

​

강체가 원점을 중심으로 반시계 방향으로 만큼 회전한다고 생각했을 때, 반지름 r만큼 떨어진 점 P에는 접선속도(tangential velocity)가 있다. 접선속도는 벡터량으로 접선속도의 크기인 접선속력은 다음과 같이 정의한다.

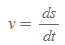
• s는 x-축으로부터 반시계 방향으로 움직인 호의 길이이다.
• 호의 길이공식: s = rθ ⇒ [그림 4]에서 호의 길이는 점선 강체의 처음 P점에서, 이동한 실선 강체의 나중 P점까지의 호의 길이를 의미한다.

​

접선속력에 호의 길이 공식을 대입하면 아래와 같이 접선속력을 새롭게 정의할 수 있다.

 

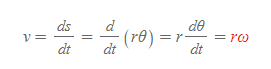
접선속력 | Linear Speed

■

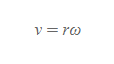
• 강체 내의 모든 점의 각속력 ω은 일정하다. cf. 그러나 강체 내의 접선속력은 회전반경에 따라 각기 다르다.

​

예를 들어 막대기를 휘두를 때 막대의 끝 접선속력이 막대의 손잡이 접선속력보다 훨씬 빠르다. ⇒ ω의 값은 모두 같으나, r은 막대로부터 멀어질수록 그 값이 커진다.

​

접선가속도

회전강체에서의 한 점의 병진가속도의 접선 성분은 회전축으로부터 그 점까지의 수직거리에 각가속도를 곱한 값과 같다.

​

접선가속도

■

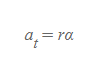
구심가속도

한편 강체의 회전 역시 회전축을 중심으로 한 원운동의 일종으로 구심가속도 a_c가 발생한다.

 

우선 원운동에서 구심가속도는 다음과 같이 정의했다.

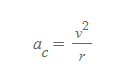
이 구심가속도 식에 접선속력을 대입하면 각속력으로 표현한 구심가속도를 새롭게 정의할 수 있다.

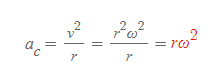
구심가속도

■

 

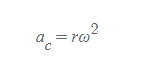
원형 경로를 따라 회전하는 한 점은 지름 가속도 벡터 a_r을 갖는다. 여기서 지름 가속도 벡터의 크기 a_r은 v^2/r이고 회전중심을 향한다. 이때 구심가속도 a_c는 지름 가속도의 크기와 같다.

 

그림 5. 접선가속도와 구심가속도 [University Physics Volume 1, OpenStax, 2016, p.511]

 

 

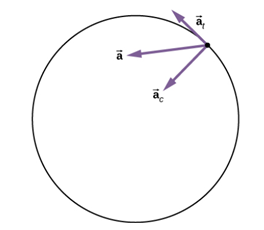
구심가속도와 접선가속도가 시작되는 지점에서의 실제 가속도는 두 가속도의 벡터합[그림 5]과 같다.

​

강체의 실제가속도

■

​

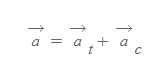
실제 가속도의 크기는 마찬가지로 벡터의 성분 합을 해주면 쉽게 계산된다.

​

실제가속도 크기

 

■
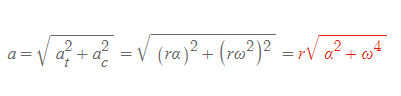