【미분적분학 2】 Chapter 4. 미적분학의 기본정리


뉴턴의 스승 배로(Isaac Barrow, 1630~1677, 잉글랜드)는 미분 문제와 적분 문제가 서로 밀접함을 발견했다.
- 배로는 접선 문제와 넓이 문제의 풀이가 서로 역과정임을 확인했다. ⇒ 미적분학의 기본정리 이전에 적분은 합의 극한으로서 계산되었다.
함수 f가 구간 [a, b]에서 적분가능하고 Δx=b-a/n, x_i=a+iΔx일 때, 정적분은 다음과 같이 정의한다.
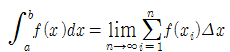
미적분학의 기본정리
미적분학의 기본정리 1(Fundamental Theorem of Calculus 1, FTC1)
만약 f가 구간 [a, b]에서 연속한다면,
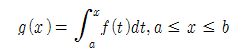
로 정의된 함수 g는 구간 [a, b]에서 연속이고, 구간 (a, b)에서 미분가능하며, g'(x)=f(x)이다.
■
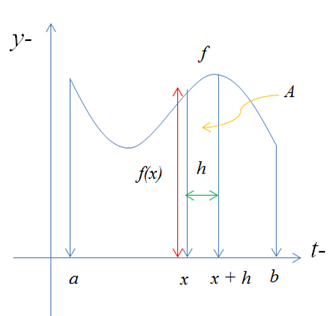
- g(x)는 f(t)의 넓이와 같다.
- g는 적분에서 상한의 변수인 x에만 영향을 받는다.
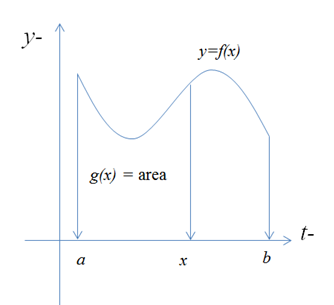
- 만약 x가 고정된 값이라면, g(x)의 값은 하나의 수가 된다. 반면, x가 변하면 g(x)의 값도 변하므로 g(x)는 x의 함수로 정의할 수 있다.
a와 b의 크기관계에 따라 다음과 같은 정적분의 관계를 갖는다.
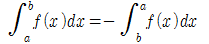
- 만약 a=b이면 Δx=0이므로, g(x)는 0이다.
함수 g의 도함수를 그리면 f를 얻을 수 있다. ⇒ g'=f
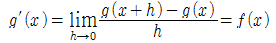
미적분학의 기본정리 2(Fundamental Theorem of Calculus 2, FTC2)
만약 f가 구간 [a, b]에서 연속이면,
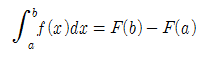
이다.
■
- F는 f의 임의의 원시함수이고, F'=f의 성질을 갖는다.
- 도함수가 f로 알려진 함수 F가 존재한다면, F를 원시함수 또는 역도함수(anti-derivative)라 한다.
구간 I상의 모든 x에 대해 F'(x)=f(x)라면, 함수 F를 구간 I상의 f의 역도함수라 한다.
- 원시함수는 ∫f(x)dx로 표현하고, 이를 부정적분(indefinite integral)이라 부른다.
부정적분
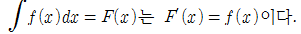
■