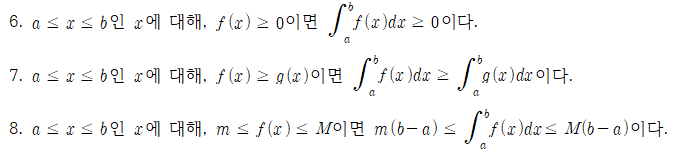【미분적분학 2】 Chapter 5. 부정적분

미적분학의 기본정리 2에서 F는 f에 대한 임의의 원시함수였고, F는 다시 ∫f(x)dx로 표현할 수 있다.
- 원시함수는 부정적분(indefinite integral)이라 불리며, 함수족(family)이다. ⇒ 즉, 부정적분은 하나의 함수족이다.
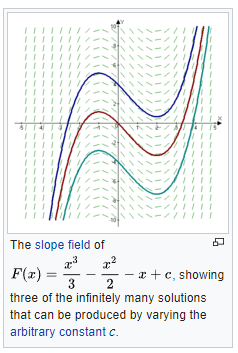
F(x)=x^3/3은 f(x)=x^2의 역도함수, 즉 부정적분이며 여러 개의 부정적분을 갖는다.
- c는 부정적분의 상수(constant of integral)이다.
- 부정적분의 상수는 임의의 값을 갖는다.
자주 사용되는 함수-부정적분 공식
함수의 미분공식처럼 앞으로 적분을 풀기 위해서는 부정적분표가 필요하다.

부정적분의 여러 공식은 우변의 함수를 미분하여 피적분함수를 구하는 것으로 증명할 수 있다.
※ List of Integrals
There are nine lists of integrals and some books, such as 'Table of Integrals, Series, and Products' contain a large collection of results.
- The first publication of the book was in 1943 and it was considerably expanded and soon became a 'classic'.
- The first edition was authored by Ryzhik and it contained about 5,000 formulas.
- It is highly regarded reference for mathematicians, scientists, and engineers.
- Language: Russian, German, Polish, English, Japanese, Chinese

1. List of integrals of rational functions
2. List of integrals of irrational functions
3. List of integrals of trigonometric functions
4. List of integrals of inverse trigonometric functions
5. List of integrals of hyperbolic functions
6. List of integrals of inverse hyperbolic functions
7. List of integrals of exponential functions
8. List of integrals of logarithmic functions
9. List of integrals of Gaussian functions
또한 미적분학의 대표 교과서인 James Stewart의 『미분적분학(Calculus)』에는 문제 풀이를 위한 24개의 필수 부정적분을 제시하고 있다.

적분의 일반성질
적분 계산에 도움이 되는 적분의 일반성질은 크게 8가지로 정리할 수 있다.
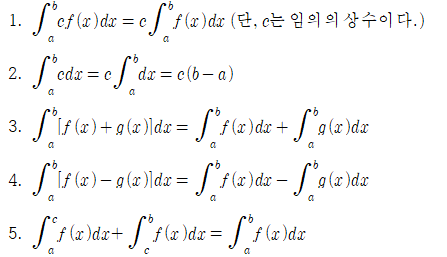
적분의 일반성질은 a, b가 어떠한 대소관계를 갖던 참이다. 그러나 크기를 비교하는 다음 성질은 a≥b 일 때만 참이다.