Herald-Lab
【수리심리학】 02. 인간의 주관적 지각: 페히너의 법칙 본문

이전 챕터에서 우리는 베버의 법칙이 어떻게 적용되는 지 간단히 확인해 보았다.

독일의 물리학자였던 구스타프 페히너(Gustav T. Fechner, 1801-1887)는 베버의 아이디어에 영감을 받아 그가 발견한 것들을 수식화 하려고 노력했다. 그리고 1860년 『Elemente der Psychophysik』 (정신물리학)을 발간하면서 페히너는 자신의 발견들을 아래와 같이 나열하였다.
- 신체적 사실(bodily facts)과 의식적 사실(conscious facts)은 서로 완벽하게 환원될 수 없다. 그러나 둘 사이의 일관된 논리성은 수학적 관계(mathematical relation)으로 표현될 수 있다.
인간의 주관적 감각의 정도(강도)가 산술적으로 증가하기 위해서는, 가해지는 자극의 크기는 기하학적으로 늘어나야 한다.
- 구스타프 T. 페히너In order that the intensity of a sensation may increase in arithmetical progression, the stimulus must increase in geometrical progression.

페히너의 법칙
Fechner's Law
페히너는 자신의 저서에서 베버의 법칙을 인용하며, 새로운 공식을 제시했다.
페히너의 법칙
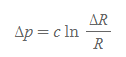
■
<물리량>
- Δp: 인간의 주관적인 감각차이(지각)
- c: 상수 (자극의 종류에 따라 다름)
- ΔR: 자극의 변화량
- R: 두 개의 비교하려는 자극량 중 작은 값
페히너의 법칙을 실제 상황에 응용하기 위해 다음과 같은 상황을 가정하자.

[1] 완벽하게 어두운 방안에 [그림 1]과 같이 촛불 하나를 두었을 때, 이 촛불을 인식할 것이고 이 촛불은 '식별가능한 자극'이라 할 수 있다.

[2] 다음, [그림 2]와 같이 촛불을 3개 두었을 때, 우리는 촛불에 의한 밝기 뿐만 아니라 그 밝기가 [그림 1]의 촛불 1개보다 더욱 밝다라는 상대적인 감각차이(지각) 또한 함께 판단할 것이다. 이때 상대적인 감각차이를 지각한 값을 Δp라 하고 이를 페히너의 법칙 공식에 적용하면 다음과 같다.
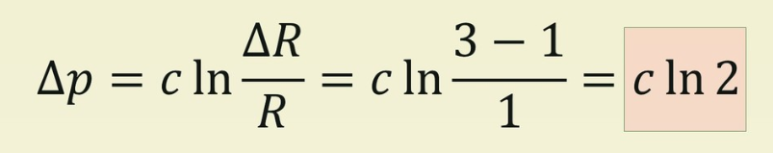

[3] 다음, [그림 3]과 같이 7개의 촛불을 두었을 때, 페히너의 법칙을 적용하면 우리는 상대적인 감각차이를 아래와 같이 계산할 수 있다.
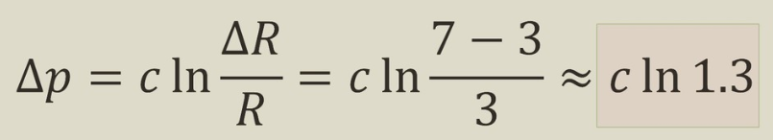
- 상황: 촛불이 3개인 방에서 4개를 더 추가하였다.
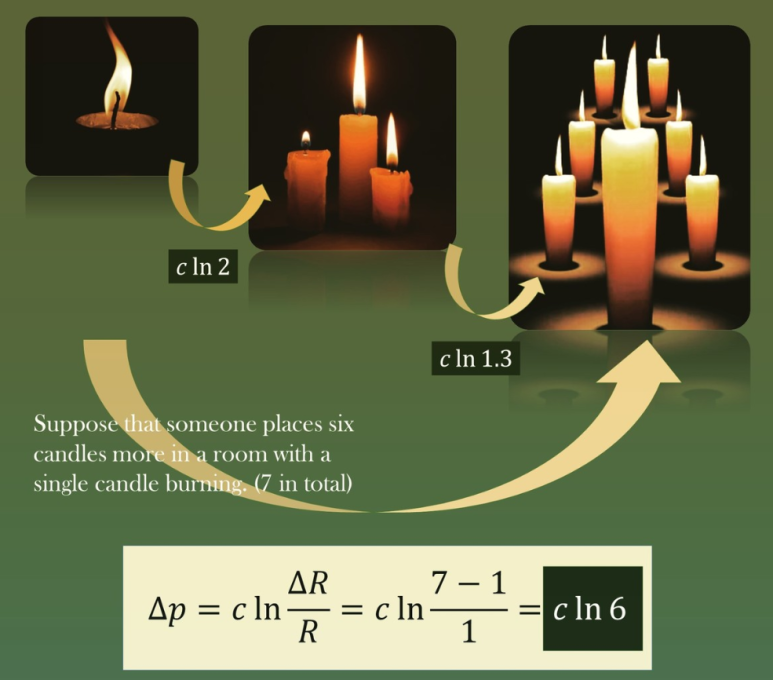
[4] 마지막으로 촛불을 한 개에서 일곱 개까지 늘였을 때의 Δp는 [그림 4]와 같이 계산할 수 있다. 그리고 위의 모든 상황은 아래 표와 같이 정리된다.
|
실험
|
촛불 개수 변화량
|
자극 크기의 알짜 변화량
|
결과 (단, 상수 c를 1로 둠)
|
|
1
|
1 → 3
|
+2
|
약 0.69
|
|
2
|
3 → 7
|
+4
|
약 0.26
|
|
3
|
1 → 7
|
+6
|
약 1.79
|
실험의 결과 값은 아래와 같이 해석한다.
- 사람들은 실험 1과 같은 상황 변화에서 이전보다 약 69%(0.69배) 더욱 방이 밝아졌음을 지각한다.
- 사람들은 실험 2와 같은 상황 변화에서 이전보다 약 26%(0.26배) 더욱 방이 밝아졌음을 지각한다.
- 사람들은 실험 3과 같은 상황 변화에서 이전보다 약 179%(1.79배) 더욱 방이 밝아졌음을 지각한다.
또한 두 실험 간의 비교를 통해 다음 내용 또한 유추할 수 있다.
- 실험 1과 실험 2 사이에는 자극의 크기가 2배 증가(+2 → +4)했다. 그러나 둘 사이에 자극의 강도 변화에 대해서는 오히려 둔감(69% > 26%)해졌다.
- 초기 자극 크기가 작을 때, 후속 자극의 크기가 대수적으로 클수록 결과(주관적으로 느끼는 감각의 차이(지각)) 또한 크다. 그러나 자극 크기의 알짜 변화량과 감각 지각은 수학적으로 비례하진 않다.
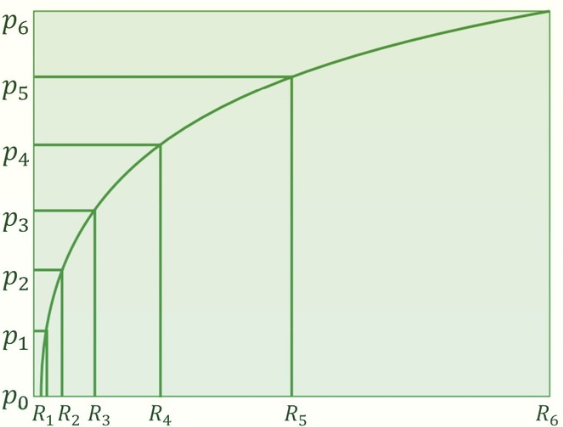
자극의 알짜 변화량(ΔR)과 주관적 감각차이(Δp)를 그래프로 나타내면 대략적으로 [그림 5]와 같이 표현할 수 있다.
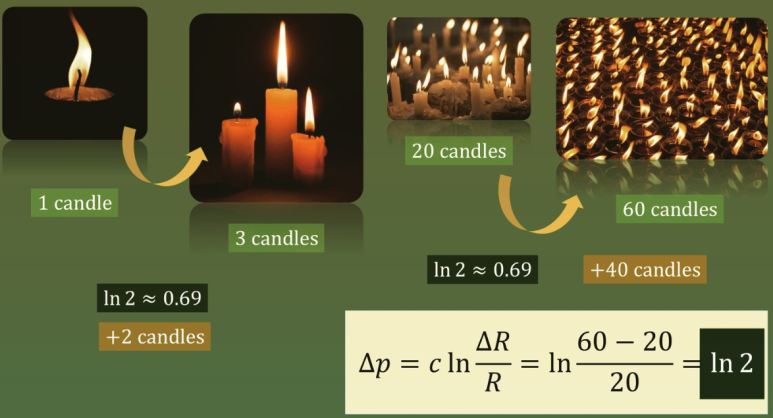
페히너의 법칙에 따르면, 사람은 어두운 방안 양초가 한 개 있는 방에서 2개를 더 갖다 놓았을 때의 밝기 변화와 20개의 양초가 있는 방에 40개를 더 놓았을 때의 밝기 변화를 거의 같다고 인지한다.
인스타그램 영문 포스팅: https://www.instagram.com/p/DTo_26ykosP/?utm_source=ig_web_copy_link&igsh=MzRlODBiNWFlZA==
로그인 • Instagram
www.instagram.com
'심리학' 카테고리의 다른 글
| 【수리심리학】 03. 노력의 배신? 연습의 멱법칙(Power Law) <PART 1> (0) | 2026.01.25 |
|---|---|
| 【수리심리학】 01. 베버의 법칙 (0) | 2026.01.19 |
| 【Artificial Intelligence / 인공지능학】 인공신경망의 기초 (0) | 2021.11.06 |
| 상관분석, 회귀분석, 선형회귀 (0) | 2021.11.06 |
| 인공지능에 관하여 (0) | 2021.11.06 |





