Herald-Lab
【수리심리학】 03. 노력의 배신? 연습의 멱법칙(Power Law) <PART 1> 본문

무언가를 잘하기 위해서는 노력이라는 요소가 반드시 필요하지만, 이 노력의 양이 만족할만한 성취를 보장하지 않음 또한 우리 모두는 경험적으로 이미 알고 있다. 수리심리학의 수학적 접근이 가능한 분야 중 학습에서는 이러한 노력(연습)이 반드시 좋은 결과로만 이어지지는 않음을 간접적으로 시사한다.
학습과 안정화
Learning and Stabiility

1926년, 미국의 응용심리학 저널(Journal of Applied Psychology)에 「학습과 안정화」(Learning and Stability) (Snoddy, 1926)이라는 글이 기고되었다. 글의 핵심은 특정한 과제 수행을 위한 연습 횟수와 실제 수행에 걸리는 시간의 관계를 수학적으로 나타낸 것으로, 저자는 실험을 통해 사람들이 연습 초기에는 수행 능력이 급격히 향상되나 연습이 지속될수록 향상 속도가 점점 느려짐을 관찰하였다.
- 수행과제는 운동 학습(motor learning) 과제로 반복 연습을 통해 어떻게 안정화(stability)
- 학습의 결과를 목표 행동의 완벽한 수행(completion time)으로 두었을 때, 학습이 한 번에 일어나는 것인지 아니면 점진적으로 나타나는 지 그래프로 나타낼 수 있다.

실험을 진행했던 심리학자 스노디는 학습단계에서 시행착오가 어떻게 숙련도로 이어지는 지를 정량적으로 알아보고 싶었다. 그래서 그는 거울에 비친 모습만으로 그림을 따라 그리는 ‘거울 그리기 과제’[그림 1]를 고안했다. 실험 참가자는 직접 자신의 눈으로 손과 펜을 보지 못한다. 대신 거울을 통해 간접적으로 자신의 행동을 관찰할 수 있고, 과제는 주어진 복잡한 모양(주로 별 모양)을 왜곡된 거울 상에서 그대로 표현해내는 것이다.
거울 그리기 과제
거울 그리기 과제 실험은 다음과 같은 특징 및 규칙을 따른다.
- 실험에 사용되는 거울은 약간의 왜곡된 상을 갖는다. ⇒ 너무 쉬운 과제에서는 연습에 따른 진행 정도를 분간하기 어렵다.
- 실험 참가자는 오로지 거울을 통해서만 자신의 행동과 그 결과를 관찰할 수 있다.
- 실험 참가자는 [그림 2]와 같은 별 모양을 그린다.
- 특징: 일반적인 손-눈 협응 운동보다 고난이도의 비자연적 운동과제이다. 또한 반복 시행이 가능하고, 연습에 의한 학습의 효과도 뚜렷하다.
또한 거울 그리기의 관찰 요소는 다음과 같다.
- 오류 횟수
- 완성 시간(과제 수행 완료)
- 시행 횟수


실험 참가자는 자신의 눈으로 직접 손을 보지 못할 뿐만 아니라 거울은 왜곡된 상으로 나타나기 때문에 초기 따라그림(트레이싱, tracing)은 오류가 많았다. 하지만 대다수의 참가자들은 반복하여 동일한 과제를 수행하면서 점점 그 상황에 익숙해졌고, 나중에는 비교적 빠르고 정확하게 과제를 수행할 수 있게 되었다.
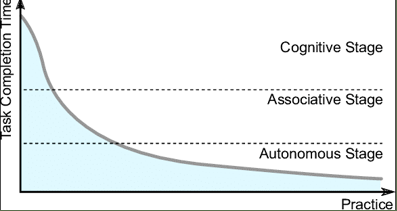
- Snoddy는 [그림 3]와 같이 연습의 횟수와 과제 수행 시간(task completion time, respond time)을 그래프로 그렸다.
- 초기 학습을 통해서 과제 수행 시간은 급격히 떨어진다.
- 그러나 어느 시점에서 과제 수행 시간의 감소폭은 줄어든다.
- 각 시행마다 작은 개선은 반드시 일어나며 거의 멈추지 않는 경향성을 띤다.
x축은 연습의 횟수, y축은 과제 수행 (완료)시간을 나타낸다.
- x축은 무차원, y축은 시간 단위를 갖는다.
Snoddy는 이렇게 줄어드는 경향성에 대해서 아래와 같이 정량적으로 표현했다.
연습의 멱법칙
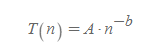
■
<물리량>
- T(n): n번째 시도에서 과제 수행 시간
- A: 초기 과제의 어려움을 반영한 상수
- n: 과제(trial, practice) 시행 횟수
- b: 과제 수행 향상률, 0과 1 사이의 상수
연습의 멱법칙은 [그림 3]과 같이 측정이 가능한 양들을 수집하여 경험적으로 작성한 식이다.
- 연습의 멱법칙 식은 (1)오류 횟수, (2)완성 시간, (3)시행 횟수 등 정량화된 데이터들을 수집하여 연습량에 따른 기대 수행시간을 예측한다.
연습의 멱법칙 공식 활용
새로운 언어 자판 키보드를 타이핑하는 방법을 배우고 있다고 하자. 처음에는 한 문장(sentence)을 쓰는 데도 아주 많은 시간을 쓸 것이다.
예를 들어 한 문단(paragraph)을 입력하는 데 60초가 걸린다고 하자. 하지만 100번의 지속적인 연습 후, 101번째 시도에서는 같은 문단을 쓰는 데 10초밖에 걸리지 않는다. 연습의 멱법칙 식에 따르면,
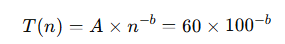
이고, T(n)은 10을 대입할 수 있다.
- A: 초기 과제의 어려움으로 첫 문단을 입력할 때 값이 이를 반영한다.
- n: 과제 수행 횟수로 이미 연습이 완료된 횟수를 대입한다.
- T(n): 101번째 시도에서 과제 수행 시간
연습의 멱법칙에서 b는 과제 수행 향상률로 다양한 원인을 갖기 때문에 미지수로 둔다. 다만 여러 번의 연습 시행에 따라 아래의 식과 같이 그 값을 유추할 수 있고, 이 값에 따라 [그림 3]의 멱함수 기울기가 결정된다. 과제 수행 향상률 b는 아래와 같이 쉽게 계산된다.
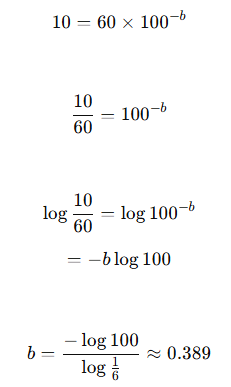
위에서 설명했던 것과 같이 b는 0과 1의 값을 갖는다. 그리고 b의 값에 따라 [그림 4]와 같은 그래프 양식을 갖는다.
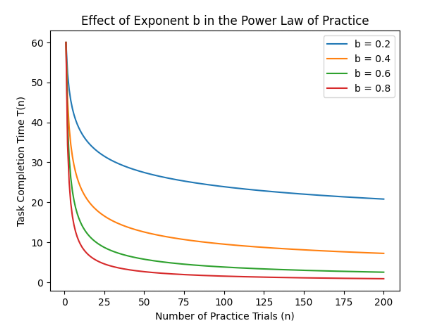
- b값이 작으면 곡선이 완만하나, 그 값이 커질수록 초기의 감소폭이 매우 크다. ⇒ 일반적으로 b는 0.2에서 0.5 사이의 값을 갖는다고 알려져있다.
인스타그램 영문 포스팅
https://www.instagram.com/p/DT47PHlkmLe/?utm_source=ig_web_button_share_sheet&igsh=MzRlODBiNWFlZA==
'심리학' 카테고리의 다른 글
| 【수리심리학】 02. 인간의 주관적 지각: 페히너의 법칙 (0) | 2026.01.21 |
|---|---|
| 【수리심리학】 01. 베버의 법칙 (0) | 2026.01.19 |
| 【Artificial Intelligence / 인공지능학】 인공신경망의 기초 (0) | 2021.11.06 |
| 상관분석, 회귀분석, 선형회귀 (0) | 2021.11.06 |
| 인공지능에 관하여 (0) | 2021.11.06 |





