
들어가기
Introduction
미분방정식(differential equation, DE)이란, 미지의 함수와 그 도함수로 구성된 식으로 미분방정식의 풀이는 자연과학, 경제학 등 다양한 현상을 모델링하는 데 필수적으로 활용되는 기술이다.
- 현실에서의 자연현상은 함수가 무엇인지는 모른 채 함숫값과 변화율만이 주어지고, 이를 통해 원함수(원래 함수)를 추리해야하는 경우가 대부분이다.
- 상미분방정식(ordinary differential equation, ODE): 미지의 함수가 일변수인 상미분항만을 포함한 DE
- 편미분방정식(partial differential eqaution, PDE): 미지의 함수가 두 개 이상의 변수를 갖고, 이에 관한 편미분항을 포함한 DE
상미분방정식은 구하려는 함수가 1개의 독립변수만을 가지는 반면, 편미분방정식은 여러 개의 독립변수로 구성된 함수와 그 함수를 편미분으로 연관된 방정식이다.
미분방정식에 포함된 도함수 중 미분 횟수가 가장 많은 것이 n번이라면 이 식을 n계 미분방정식이라 칭한다.
- 계수(order): n계 미분방정식의 수 n

위의 주어진 1계 방정식에 아래의 식을 대입해보자.
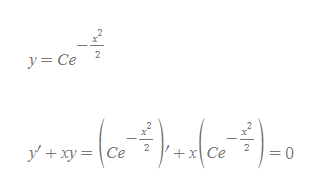
y'+xy=0에 Ce^(-x^2/2)를 대입하면 등식이 성립하는데, 이때 주어진 식 y를 미분방정식의 해(solution)라고 한다.
- 다양한 형태의 미분방정식의 해를 구하는 것이 미분방정식 학습의 주요 목표이다.
변수분리형 미분방정식
Separable ODE, Separation of Variables
변수분리법은 ODE의 풀이법 중 가장 간단한 방법으로, 핵심은 방정식에서 변수 x와 y를 분리하여 각각 따로 적분하는 것이다.
변수분리형 미분방정식은 아래와 같은 꼴을 갖는다.
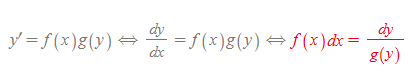
위의 경우 종속변수는 y이고, 독립변수는 x이다.
- 종속변수와 독립변수를 각각 좌변과 우변으로 분리한다.
- 단, B(y)는 0이 되면 안된다.
다음 위의 식에 대해 부정적분을 하면 아래와 같은 식을 얻을 수 있다.
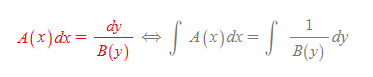
위를 풀면 독립변수 x와 종속변수 y, 그리고 적분상수로 표현되는 식을 얻을 수 있다.
예제 1.
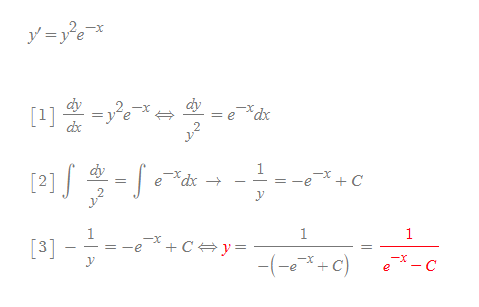
■
변수분리형 중 가장 기본이 되는 예제는 다음과 같이 요약이 가능하다.
형태
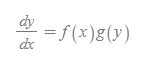
풀이
변수를 분리한 뒤 적분을 해준다.
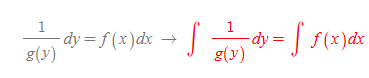
특수해
Particular Solution
임의의 상수를 사용해 모든 해를 표함한 표현을 미분방정식의 일반해(general solution)라 한다. 한편 만약 위의 부정적분의 상수값 C 대신 특정한 값을 선택할 수 있다면, 이 때 최종적으로 얻은 해는 특수해(particular solution)라 한다.
예제 2
[예제 1]에서 y(1)=3이라는 조건이 붙을 경우 특수해를 구하시오.
SOLUTION.
앞에서 이미 1/(e^-x)-C라는 일반해를 얻었으므로, 조건을 대입해본다.

적분 상수 C는 위의 식에서 빨간 색으로 표시했으며, 이를 일반해에 다시 대입하면 아래와 같다.
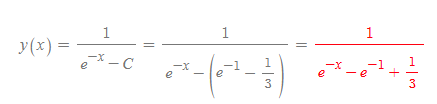
■
적분 상수 C를 규명하고 난 뒤에 이를 일반해에 대입한 것을 특수해라고 하며, 위와 같은 문제를 초기값 문제라고 한다.
예제 3
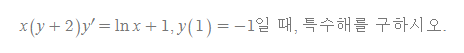
SOLUTION.
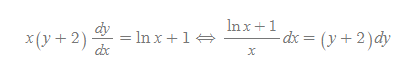
여기서 x는 0이되면 안된다는 조건이 붙는다.
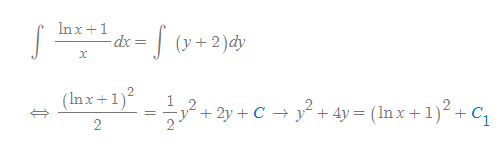
여기서 적분상수 C는 (lnx+1)^2/2의 1/2항을 없애기 위해 x2를 함으로써 C_1으로 새로 작성되었고, 따라서 두 개의 적분상수는 다음과 같은 관계식을 갖는다.
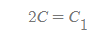
일반식 y(x)가 나왔고, 따라서 y(1)=-1을 이용해 적분상수를 실질적으로 구할 수 있다.
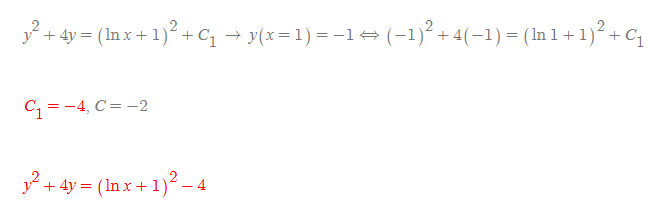
■