Herald-Lab
【물리학 - 고전역학】 27. 각속도와 각가속도 본문

강체의 회전 분석에 있어서 각속도와 각가속도는 매우 핵심적인 개념들이다.
각속도와 접선속도
Angular Velocity and Tangential Velocity
【물리학 - 고전역학】 26. 강체와 회전
강체 강체: 형태가 고정되어 변형이 없는 물체, 외력이 가해져도 모양이나 크기가 변하지 않는다. 입자들 ...
blog.naver.com
각속도
- 각속도: 강체의 각변위를 그 변위가 일어난 시간 간격으로 나눈 비율
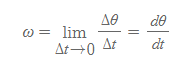
- 각속도는 일반적으로 순간 각속도를 지칭한다.
- 강체가 반시계 방향으로 돌 때, 변위는 양수 값을 갖고, 따라서 각속도 또한 양의 부호를 갖는다.

어떤 강체가 특정한 (1)각을 가지고 회전할 때 매우 짧은 시간 동안 (2)각변위와 (3)호는 벡터 물리량[그림 1]으로 다음 식을 만족한다.
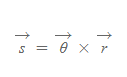
<물리량>
- s: 호
- θ: 각, 물체가 회전할 때 돌아간 정도
- r: 회전축인 원점으로부터 떨어진 거리
<의미>
호는 각도 벡터와 위치 벡터의 외적(벡터곱, cross product)이다.
접선속도
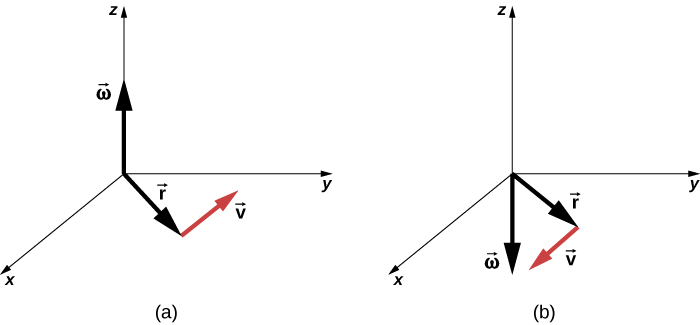
어떤 강체가 매우 짧은 시간 각을 가지고 회전하는 순간, 그 강체의 어떤 요소는 접선속도(tangential velocity) v_t[그림 2]를 갖는다.
- 각속도는 각변위를 시간 간격으로 나눈 값이라면 접선속도는 호를 시간 간격으로 나눈 값이다.
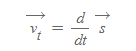
여기서 s는 위에서 언급한 호 벡터로 cross vector를 대입하면 아래와 같이 계산할 수 있다.
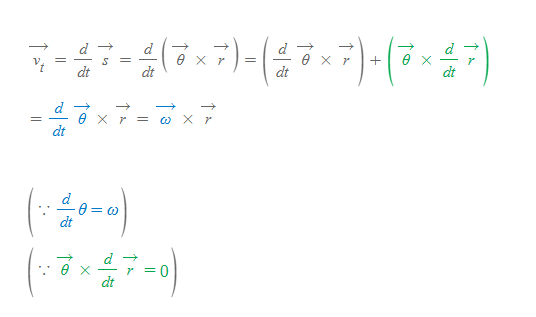
접선속도 v_t는 cross vector의 미분 결과로 다음과 같은 값을 갖는다.
접선속도
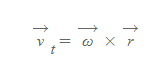
■
<물리량>
- v_t: 접선속도(벡터)
- ω: 각속도 벡터
- r: 회전축인 원점으로부터 떨어진 거리 벡터
또한 원호 s를 rθ로 두었을 때 접선속도의 크기인 접선속력(tangential speed)을 구할 수 있다.
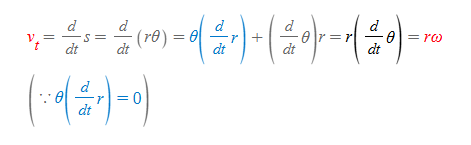
접선속력

■
<물리량>
- v_t: 접선속력
- ω: 각속도
- r: 회전축인 원점으로부터 떨어진 거리
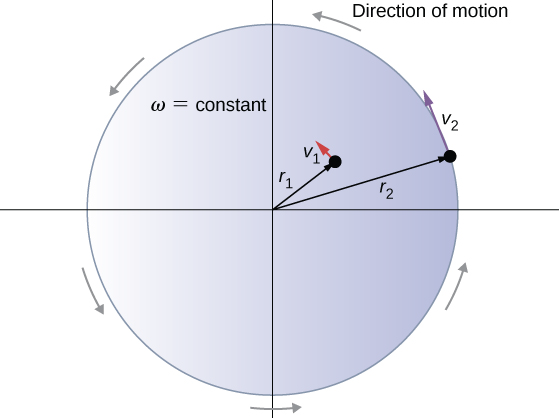
[그림 3]과 같은 원판 강체에 요소 1과 2를 설정하였을 때, 각속도 ω는 지점에 상관없이 모두 일정(constant)하다. 그러나 반지름이 큰 지점(1<2)의 요소가 접선속력 수식에 따라 더 큰 접선속력을 가짐을 알 수 있다.
각가속도
Angular Acceleration
어떤 물체의 직선 운동에서 가속도를 가지면 그 물체의 속도가 변한다. 마찬가지로 강체의 각속도는 각가속도를 가질 때 변한다.
- 각가속도 또한 (1)평균 각가속도(average angular acceleration)와 (2)순간 각가속도(instantaneous angular acceleration)로 나뉜다.
평균 각가속도
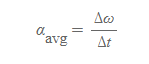
■
<물리량>
- α: 각가속도
- ω: 각속도
- Δt: 시간 간격
<의미>
각속도의 변화에 시간간격을 나눈 값
<단위>
[rad/s^2]
평균 각가속도의 시간간격이 0으로 접근할 때, 평균 각가속도의 극한 값을 순간 각가속도로 정의한다.
순간 각가속도
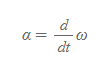
■
각속도와 마찬가지로 각가속도 또한 일반적으로 순간 각가속도를 의미한다.
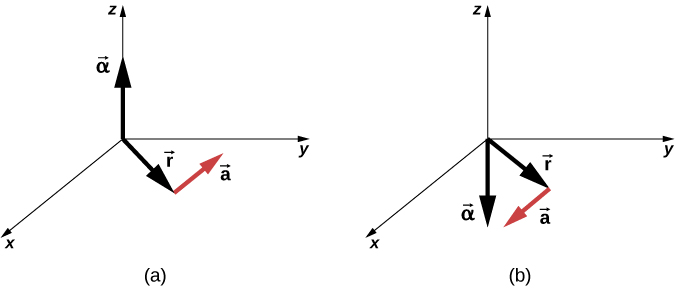
각가속도가 양의 부호를 갖는 조건은 다음과 같다.
- 반시계 방향으로 회전하는 강체가 빨라지는 경우
- 시계방향으로 회전하는 강체가 느려지는 경우
각가속도와 각속도의 방향이 서로 같을 때, 강체의 회전은 빨라진다. 반면 각가속도와 각속도의 방향이 서로 다를 때는 강체의 회전이 느려진다[그림 4].

접선가속도
접선속도 v_t 식에 시간에 대한 미분을 하면 접선가속도 a_t를 구할 수 있다.
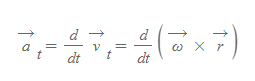
위 식의 cross vector 미분을 하면 접선가속도 식에서 각가속도의 벡터 식을 유도할 수 있다.
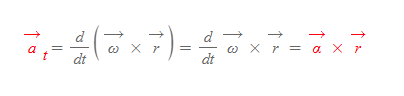
접선속력 v_t를 미분하면 접선가속도 a_t를 구할 수 있다.
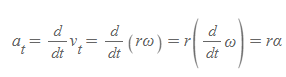
접선 가속도
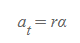
■
'물리학 > 고전역학' 카테고리의 다른 글
| 【물리학 - 고전역학】 29. 보존력 (0) | 2025.10.26 |
|---|---|
| 【물리학 - 고전역학】 28. 질량 중심 (0) | 2025.09.14 |
| 【물리학 - 고전역학】 26. 강체와 회전 (0) | 2025.09.12 |
| 【물리학 - 고전역학】 25. 퍼텐셜에너지 (0) | 2025.08.25 |
| 【물리학 - 고전역학】 24. 운동에너지 (0) | 2025.08.22 |




