Herald-Lab
【물리학 - 고전역학】 29. 보존력 본문

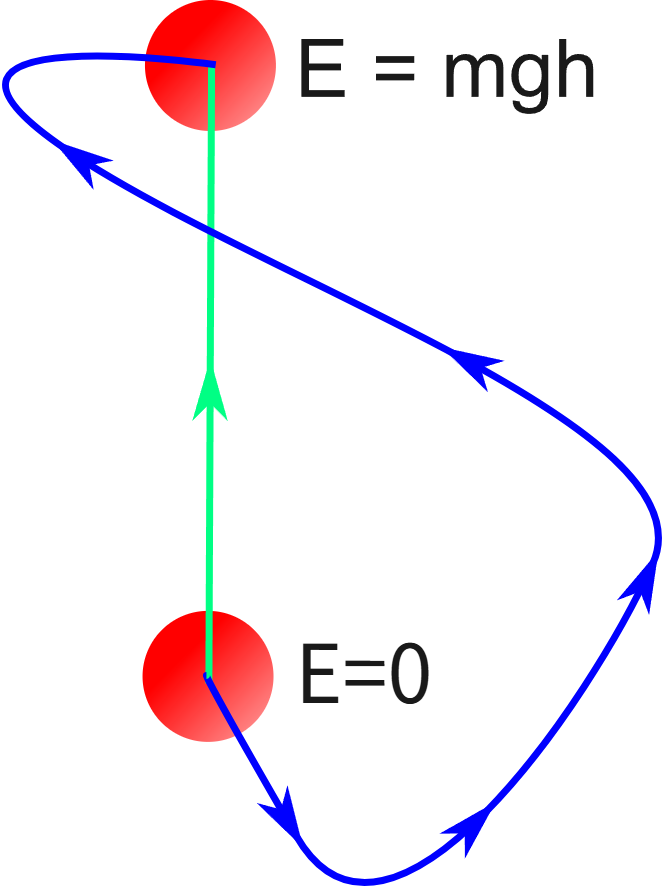
[그림 1]과 같이 중력이 한 일은 물체가 이동한 경로와 상관없이 오로지 높이에 의해서만 결정된다. 이렇듯 경로에 의존하지 않는 힘을 고전역학에서는 보존력이라 한다.
보존력(conservative force): 어떤 물체를 한 점에서 다른 점으로 옮기는 데 드는 일이 그 물체의 이동경로와는 무관한 힘[그림 2]
- 보존계(conservative system): 보존력만이 작용하는 시스템
중력의 경우, 높이가 h인 연직방향에서의 물체의 퍼텐셜에너지나, 높이가 h인 빗면에서의 물체의 퍼텐셜에너지는 본질적으로 동일하다.

보존력에 해당하는 대표적인 힘들로 중력, 용수철 탄성력, 전자기력을 들 수 있다.
보존력의 성질
보존력은 크게 아래와 같은 2가지 성질로 설명된다.
- 두 점 사이를 이동하는 입자에 보존력이 한 일은 이동경로(path)와 무관하다.
- 닫힌 경로를 따라 이동하는 입자에 보존력이 한 일은 0이다.
여기서 닫힌 경로(closed path)란, 출발점과 도착점이 서로 같은 경로를 뜻한다.
또한, 닫힌 경로 테스트*를 통과하는 힘은 보존력으로 분류된다.
|
닫힌 경로 테스트
어떤 물체가 A지점에 놓여있고 여기에 힘 F가 작용한다고 하자. 물체는 힘에 의해 여러가지 경로를 가질 수 있는 데, 우연히 A지점을 다시 지난다고 하면 그 순간까지 이 힘 F가 한 일의 총량은 0이 된다. 이 힘 F는 닫힌 경로 테스트를 통과한 것이며, 따라서 힘 F는 보존력으로 분류된다.
|
보존력과 퍼텐셜에너지
Conservative Force and Potential Energy
어떠한 시스템의 구성요소가 이전과 다른 배열상태를 가졌을 때 우리는 그 시스템이 퍼텐셜에너지를 갖는다라고 표현했다. 계의 구성 요소들이 가질 수 있는 배열상태의 변화로 위치의 이동과 회전 등이 있는데, 중력 퍼텐셜에너지를 다시 예로 들어보자.
질량이 m인 물체에 외력 F_ext을 작용해 지표면 y=0으로부터 특정한 위치 y_f까지 일정한 속도로 들어 올릴 때, 외력이 한 일은 다음과 같다.
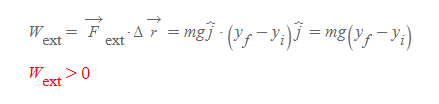
- 질량 m은 일정한 속도로 움직이기 때문에 외력과 중력의 크기는 서로 같을 것이다. 따라서 외력 F_ext의 크기를 mg로 적을 수 있다.
- 단위벡터 j 끼리의 dot cross는 그 값이 1이다.
- 외력의 방향과 물체의 이동방향이 같기 때문에 외력이 한 일은 양의 부호를 갖는다.
또한 앞선 챕터에서 중력 퍼텐셜에너지를 mgy로 정의했기 때문에 위의 식을 정리하면 다음과 같다.
일정한 속력으로 물체를 들어 올릴 때 외력이 한 일
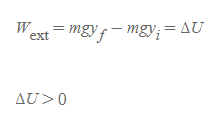
■
한편 질량 m인 물체에 작용한 중력 F_g는 물체의 이동방향과 정반대이기 때문에 중력이 한 일은 다음과 같다.
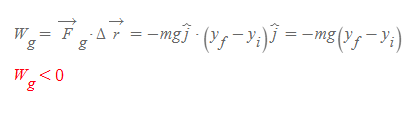
일정한 속력으로 물체를 들어 올릴 때 중력이 한 일
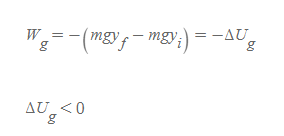
■
지표면으로부터 물체를 들어올렸을 때 중력이 한 일은 (-)부호를 갖고 이는 수식적으로 마이너스 퍼텐셜에너지의 변화량으로 정의된다. 즉, 보존력이 한 일은 마이너스 보존력 퍼텐셜에너지의 변화량과 같다.
보존력이 한 일
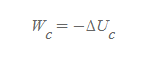
■
임의의 경로를 x축이라 가정했을 때, 보존력이 한 일에서 위치에너지의 변화량 ΔU를 다시 정의하면, 일의 적분식을 활용해 아래와 같이 식을 변형시킬 수 있다.
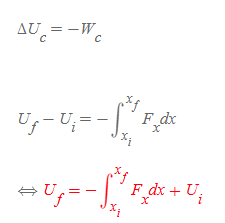
마지막으로 (1)퍼텐셜에너지가 가장 작은 지점 U_i를 0으로 잡고 (2)보존력 F를 중심으로 위 식을 정리하면 보존력의 정의를 구할 수 있다.
보존력의 정의
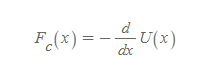
■
보존력의 정의를 통해 우리는 아래와 같은 의미를 유추할 수 있다.
- 보존력은 항상 계가 가질 수 있는 가장 작은(낮은) 위치에너지를 갖도록 작용한다.
- 보존력의 정의 식에서 음수부호는 가장 작은 위치에너지 값을 갖도록 만드는 보존력의 특성을 반영한다.
- 힘의 작용점이 작은 변위 dx만큼 움직일 때 미소 위치에너지의 변화량 dU의 비를 보존력으로 정의한다.
퍼텐셜에너지 U는 3차원 좌표계에서 (x, y, z)의 함수이며, 그로 인해 아래와 같은 일반식을 갖는다.
보존력
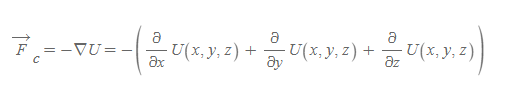
■
3차원에서 보존력은 퍼텐셜에너지의 음의 그래디언트(gradient)이고, 이는 벡터량이다.
'물리학 > 고전역학' 카테고리의 다른 글
| 【물리학 - 고전역학】 31. 중력장에서의 운동: 수평으로 던진 물체 (0) | 2026.01.11 |
|---|---|
| 【물리학 - 고전역학】 30. 중력장에서의 운동: 연직방향 (0) | 2026.01.10 |
| 【물리학 - 고전역학】 28. 질량 중심 (0) | 2025.09.14 |
| 【물리학 - 고전역학】 27. 각속도와 각가속도 (0) | 2025.09.13 |
| 【물리학 - 고전역학】 26. 강체와 회전 (0) | 2025.09.12 |





