Herald-Lab
[적분] 16장. 적분법: 부분적분 본문
미분법의 곱법칙(product rule)에 대응되는 부분적분법(integration by parts, IBP)을 알아보자.
※ The IBP
[1] Suppose that u(x) and v(x) are differentiable functions.
[2] The product rule in terms of differentials gives us:
d(uv)=udv+vdu
[3] Rearranging the rule, we can write:
udv=d(uv)-vdu
[4] Integrating both sides with respect to x:
∫udv=uv-∫vdu (integration by parts formula)
부정적분 부분적분

■
IBP에서 핵심적인 사항은 u와 dv를 적절하게 선별하는 일이다. 그리고 이런 피적분함수를 치환할 때, 경험적으로 ILATE 규약을 활용한다. ILATE란,
Inverse trigonometric
Logarithmic
Algebraic
Trigonometric
Exponential
의 첫 알파벳 글자 모음으로, 가령
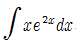
와 같이 피적분함수가 합성함수 일 때, ILATE에 근거해 u로 가능성 있는 함수를 선택한다면 algebraic 함수인 x가 exponential 함수인 e^2x보다 우선한다.

- IBP를 시행할 때, u와 dv는 피적분함수를 모두 포함하도록 설정한다.
EXAMPLE 16.1 부정적분 부분적분

□
부정적분의 부분적분에서 첨가되는 여러 적분상수들은 총합의 개념으로 마지막 결론 부분에서 간단히 C로 제시한다.
점화공식
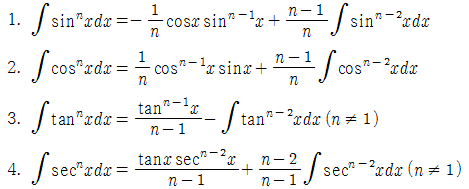
■
부분적분을 활용해 n≥2인 정수 n에 대한 점화공식을 증명할 수 있다.
정적분 부분적분
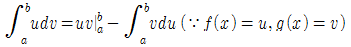
■
'Calculus > Concepts of Calculus' 카테고리의 다른 글
| [적분] 18장. 적분법: 삼각치환적분 (0) | 2019.08.31 |
|---|---|
| [적분] 17장. 적분법: 삼각함수적분 (0) | 2019.08.30 |
| [적분] 15장. 적분법: 치환적분 (0) | 2019.08.29 |
| [적분] 14장. 적분: 부정적분 (0) | 2019.08.28 |
| [적분] 13장. 미적분학의 기본정리 (0) | 2019.08.28 |




