
사인형 파동
Sinusoidal Waves
일상에서 자주 볼 수 있는 파동의 대표적인 형태로 파도[그림 1]를 들 수 있다.
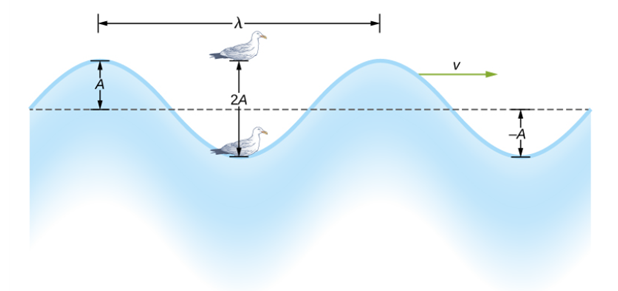
- 사인형 파동은 특정한 주기를 가지고 일정한 모양을 가지기 때문에, 위와 같이 새로운 물리량을 유추할 수 있다.
- 마루(crest): 파동의 최고점
- 골(trough): 파동의 최저점
- 파장(wavelength, λ): 한 마루에서 다음 마루까지의 거리, 혹은 한 골에서 다음 골까지의 거리
- 주기(period, T): 한 파장이 이동하는 데 걸리는 시간, 단위는 초[s]
- 진동수(frequency, f): 단위 시간 당 주어진 지점을 지나가는 마루의 총 개수
- 진폭(amplitude, A): 매질요소의 평형위치로부터 최대위치까지의 거리 혹은 최저위치(골)까지의 거리
- 사인형 파동은 연속적인 주기 파동의 가장 간단한 예로, 어떠한 복잡한 파동이라도 사인형 파동으로 분리할 수 있다. ⇒ 복잡한 파동도 결국은 시간차를 보이는 사인형 파동의 총합과 같다.
위의 파동은 위치-변위 그래프[그림 2]로도 나타낼 수 있다.
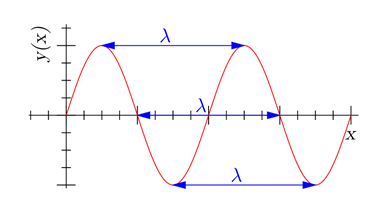
각각의 물리량에 대해 알아보자.
진동수 | Frequency
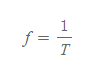
■
- 물리량
- f: 진동수
- T: 주기
- 의미: 진동수는 주기의 역수이고, 이의 반대 또한 성립한다.
- 단위: 헤르츠[Hz], 초 시간의 역수 [s^-1]이다.
주기 | Period
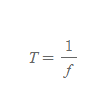
■
주기는 정확하게 진동수 식의 역수이다.
- 주기: 한 번의 진동이 발생했을 때 그 진동이 완료되었을 때까지 걸린 시간
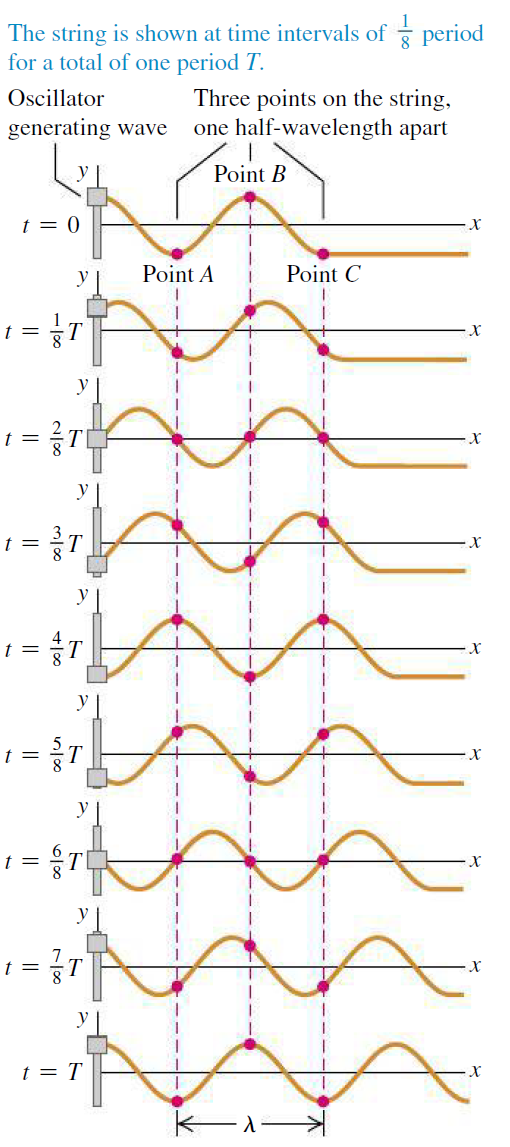
[그림 3]은 한 주기의 줄파(string wave) 진동을 1/8[초] 별로 나눈 그림이다.
일반적인 파동함수의 기술
[1] 시간이 0일 때(t=0), 펄스의 모양이 어떻든지 간에 파동은 수학적으로 다음과 같이 표현한다.
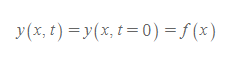
- 의미: 시간 t=0일 때, 각각의 x값에 대한 줄의 횡(세로축) 위치 y
[2] 펄스의 속력을 v라고 두고 펄스의 모양이 시간과 관계없이 항상 일정하다고 가정하면, t초 후에 파동은 다음과 같은 식을 가진다. 파동은 [그림 4]와 같이 시간에 따라 오른쪽으로 퍼진다고 하자.
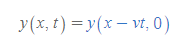
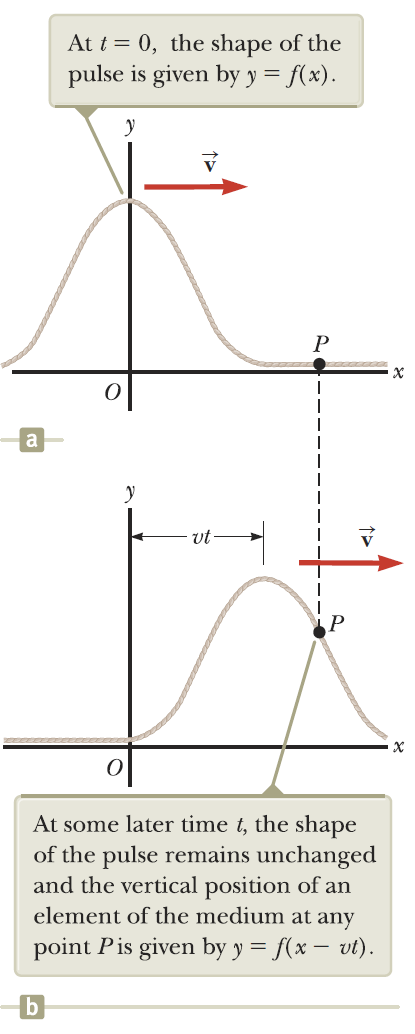
- 의미: 펄스가 vt의 거리만큼 ‘오른쪽’으로 이동한 파

파동의 속력은 항상 일정하므로, 파동이 이동한 거리는 vt라 쓸 수 있고, 파란 색 식에서 t=0인 이유는, 파동함수 f(x)는 t=0일 때 각각의 x값에 대한 줄의 횡 위치 y에만 관심이 있기 때문이다.
- y(x, t)에서 x는 t 시간만큼이 지난 지점의 횡위치 y를 뜻한다.
- y(x-vt, 0)은 시간 t일 때 수평지점 x에서의 줄의 요소 y값은, t=0일 때, 수평지점 x-vt에서의 y값과 같음을 의미한다.
y(x-vt, 0)는 t=0일 때를 기준으로 작성된 함수이다. 이 때문에 펄스가 전파되려던 시점인 t=0에서의 위치를 x-vt라고 적을 수 있다. 일반적으로 원점이 O인 정지 틀에서 오른쪽으로 움직이는 파동을 측정할 때, 모든 위치와 시간에서의 횡 위치 y는 다음과 같이 쓸 수 있다.
파동함수 | Wave Function
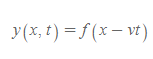
■
- 의미: 오른쪽으로 일정한 속력 v를 가지고 이동하는 펄스
- y(x, t)는 x와 t의 함수 y라고 부른다.
사인형 파동
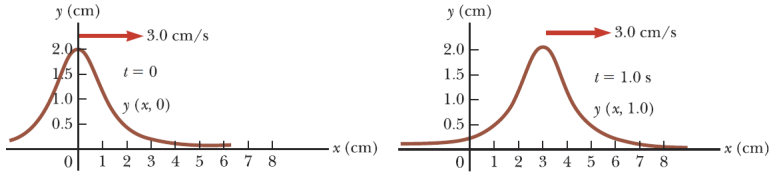
사인형 파동(사인형 파동함수, 사인파)의 공식
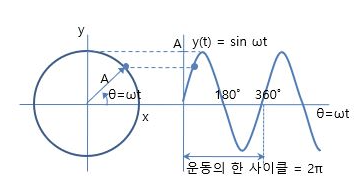
[1] t=0일 때, 파동은 사인 그래프를 그리고 있으므로 이 순간, 파동에 대한 함수는 다음과 같은 식을 따른다고 알려져 있다.
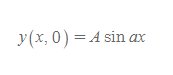
- 물리량
- A: 진폭
- a: 구해야 할 상수
x=0일 때, y(0,0)=Asin(a)(0)=0이다.
[2] y=0이 되는 다음 x값은 반파장(파장의 반쪽 길이) λ/2이다.
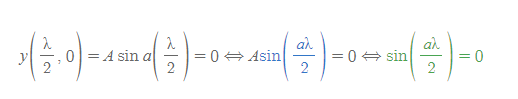
- sin(aλ/2)이 0이 되려면 sin(180)=sinπ=0이면 된다.
[3] a 구하기
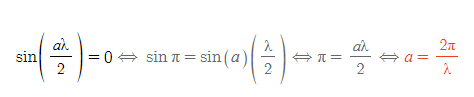
- 파동의 진폭은 항상 그 크기를 가지므로, 위의 식이 성립하기 위해서는 항이 0이 되어야 한다. ⇒ sinπ=0이므로, a는 2π/λ로 계산된다.
[4] 파동의 사인형 함수 일반식
t=0일 때 파동의 사인형 함수
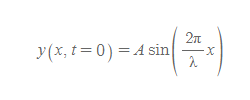
■
t를 임의로 0으로 보낼 때, 위의 식은 아래와 식과 매우 유사하다.
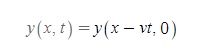
[4] y(x, t)=y(x-vt, 0)이기 때문에, x자리에 x-vt를 넣어줄 수 있다.
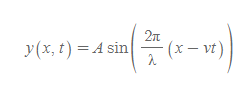
- 의미: 파동이 오른쪽으로 v만큼의 속력으로 움직일 때, 시간 t 후의 파동함수
[5] 파동의 속력 v는 [길이/시간] 차원으로 v=λ/T로 계산된다.
파동의 속력 | Speed of Wave
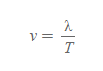
■
[6] [과정 4]의 파동방정식에 파동의 속력 식을 적절히 대입하면 사인형 파동의 일반식을 유도할 수 있다.
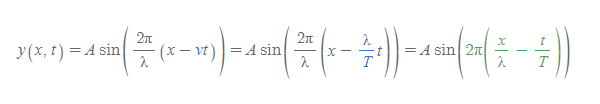
[7] 2π를 파장 λ와 주기 T와 적절히 연립하여 새로운 물리량, 파수(wave number)와 각진동수(angular frequency) 정의한다. 이 두 개념을 적용하면, 분수가 사라진 좀 더 일반적인 파동방정식을 구할 수 있다.
파수 | Wave Number
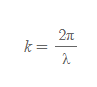
■
- 의미: 파장의 역수로 단위 길이 당 파장의 수를 뜻한다.
각진동수 | Angular Frequency
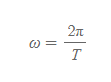
■
- 기호: ω(오메가)
- 의미: 진동수에 를 곱한 값으로 단위 시간당 물체가 움직인 각도를 뜻한다.
사인형 파동함수
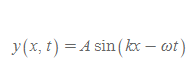
■
'고급물리학 > 음향학' 카테고리의 다른 글
| [물리학-음향학] 03. 줄에서의 파동(줄파) | Waves on a String (1) | 2023.11.15 |
|---|---|
| [물리학-음향학] 01. 음향과 파동 | Acoustic and Waves (1) | 2023.11.13 |