[물리학-음향학] 03. 줄에서의 파동(줄파) | Waves on a String

 

줄에 나타나는 사인형 파동

Sine Waves on Strings

 

그림 1

 

 

• 사인형 파동의 분석에 있어 가장 쉬운 사례는 줄의 한 쪽 끝을 묶고 횡파[그림 1]를 만들어 내는 것이다.
• 줄파에서 y축의 각각의 줄 요소는 단조화 운동[그림 2]을 한다. ⇒ 줄의 각 부분(segment)을 단순조화 진동자로 취급할 수 있다. cf. 단, 줄의 요소들은 항상 수직선상에서만 진동한다.

 

그림 2. 줄의 각 부분이 갖는 주기적 운동은 마치 용수철에 달린 작은 질량의 단조화운동처럼 간주할 수 있다.

 

 

• 횡속력(transverse speed): v_y[그림 3], 파동의 속력 v와 반드시 구분하여 사용한다.

 

그림 3. 파동의 속력 v와 횡속력 v_y, 그리고 횡가속도 a_y [출처: Sears & Zemansky's University Physics with Modern Physics, Young & Freedman, 14th ed., 2016, p.502]

 

​

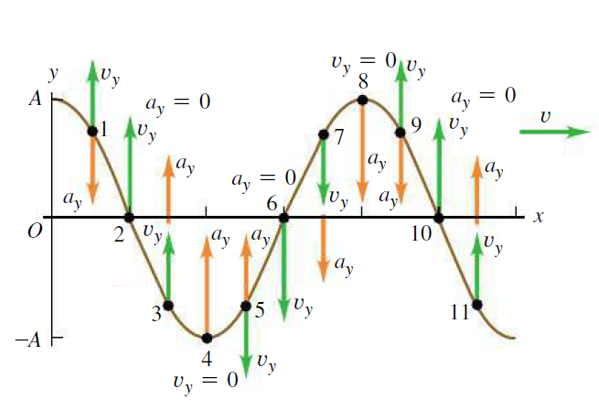
사인형 파동의 미분 물리량: 횡속력, 횡가속도

횡속력과 횡가속도는 파수 ω와 각진동수 k로 나타낸 파동함수 식을 시간에 대해 미분함으로써 각각을 구할 수 있다.

​

[1] 횡속력

• t=0일 때, 파동함수 y=Asin(kx-ωt) 식을 시간에 대해 미분한다.

• y는 x와 t의 복합함수이고, 시간 t에 대해서만 미분을 하고자 하기에 x는 상수로 두고 값을 푼다. ∂/∂t[sin(at+b)] 꼴로 미분하여 그 결과를 아래와 같이 유도할 수 있다.
• sin(ax+b)를 x에 대해 미분한 결과 값 acos(ax+b)를 활용한다.

횡속력 | Transverse Speed

 

■

​

[2] 횡가속도

• 속도의 미분은 가속도로 같은 논리를 적용해 횡속력의 미분 값을 횡가속력이라 유추할 수 있다. 단, 횡속력의 크기 변화는 벡터량인 가속도이므로 최종적으로는 그 값을 횡가속도라 정의한다.
• 마찬가지로 y는 x와 t의 복함함수 이므로, 시간 t에 대해서만 미분하면 다음과 같다.
• cos(ax+b)를 x에 대해 미분한 결과 값 -asin(ax+b)를 활용한다.

 

​

​

횡가속도 | Transverse Acceleration

 

■

횡속력과 횡가속도의 최대크기는 다음과 같다.

• 최대 횡속력: v_y, max ⇒ 변위 y=0일 때, 파동은 최대 횡속력을 갖는다.
• 최대 횡가속도: a_y, max ⇒ 변위 y=+A 또는 -A일 때, 파동은 최대 횡가속도를 갖는다.

​q.e.d.

 

줄파가 가진 에너지

Energy along a String

 

그림 4. 줄의 요소 dm이 갖는 에너지 dK

 

 

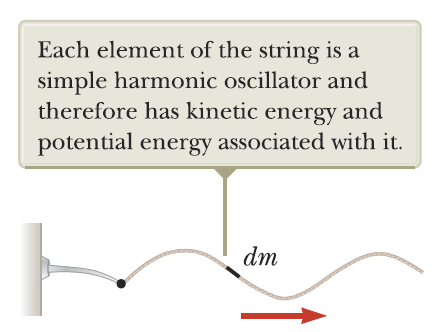
어떤 한 점에 줄을 묶고 줄의 한 점에 물체를 매단 후, 줄에 입사펄스를 보내는 경우를 떠올려 보자.

• 줄을 통해 보낸 펄스는 일차원의 사인형 파동과 같다. ⇒ 사인형 파동이 줄을 따라 진행하는 경우, 에너지원은 줄의 왼쪽 끝에서 외부에 가해준 일이므로 줄은 비고립계로 간주할 수 있다.
• 줄에 펄스가 전달되면, 매달린 물체에 이르러 물체가 일시적으로 위로 올라간다. ⇒ 물체-지구 계의 중력퍼텐셜에너지가 증가한다.

​

줄의 각 요소는 단순조화 운동을 한다.

• dx: 줄의 요소 길이
• dm: 줄의 요소 질량 ⇒ μ를 단위 길이 당 질량(dm/dx)으로 두면, 요소질량 dm=μdx로 고칠 수 있다.

​

줄의 요소는 모두 동일한 각진동수와 진폭을 갖는다. 그리고 줄의 요소 dm이 가진 운동에너지 dK[그림 4]는 다음과 같이 계산한다.

​

줄의 미소요소는 파동의 전파 방향과는 별개로 횡속력만 가지고 있기 때문에, 이것에 의해 운동에너지를 구할 수 있다.

​

횡속력의 식을 dK 식에 대입하자.

​

위의 식을 파동의 한 파장 내에 줄의 모든 요소에 대해 적분하면 한 파장 내 줄의 전체 운동에너지 K_λ(total kinetic energy of all the string)를 구할 수 있다.

​

​

위의 식에서 파수 k는 2π/λ이기 때문에 적분의 결과를 파장 λ에 대해 풀어 썼다.

​

한 파장 내 줄의 전체 운동에너지

■

또한 운동에너지 이외에, 줄의 각 요소는 평형상태로부터의 변위와 이웃하는 성분으로부터의 복원력으로 인해 퍼텐셜에너지를 가진다. 그리고 이 값은 정확하게 한 파장 내 줄의 전체 운동에너지의 값과 같다.

​

한 파장 내 줄의 전체 퍼텐셜에너지

■

​

한 파장 내의 줄의 전체 에너지는 운동에너지와 퍼텐셜에너지의 합이다.

 

한 파장 내의 줄의 전체 에너지

■

​

한 파장 내의 줄의 전체 에너지는 (1)단위 길이 당 질량과 반파장(λ/2)에 비례하고, (2)진폭과 파수에는 제곱 비례한다.