Herald-Lab
【물리학을 위한 수학】 01. 기준계와 좌표계 본문

물리학의 여러 가지 문제 상황은 공간 상에서의 위치 표현으로부터 시작되며, 이를 위하여 기준계와 좌표계를 최초로 배운다.
- 기준계(基準系, reference system, reference frame): 기준틀, 어떤 물체의 운동을 숫자로 대응할 기준을 제공하는 프레임(틀)
- 좌표계(座標系, coordinate system): 물체의 위치를 숫자로 표시할 좌표(coordinate)를 사용하는 체계
기준계와 좌표계
Reference Frame and Coordinate System
기준계와 좌표계는 해석역학에서 확실히 구분되는 개념으로 상세한 내용은 아래와 같다.
기준계
기준계는 물체의 운동을 숫자로 대표할 기준을 제공하는 틀로 물리학에서는 관성 기준계, 질량중심 기준계, 오른손 기준계 등이 자주 사용된다. 기준계 틀은 원점과 좌표축을 최초로 정함으로써 설정되는데, frame 설정 절차[그림 1]는 다음과 같다.
[1] 원점 설정
[2] 좌표축 설정
[3] 좌표축의 (+)방향 설정
[4] 좌표축의 눈금(scale) 설정
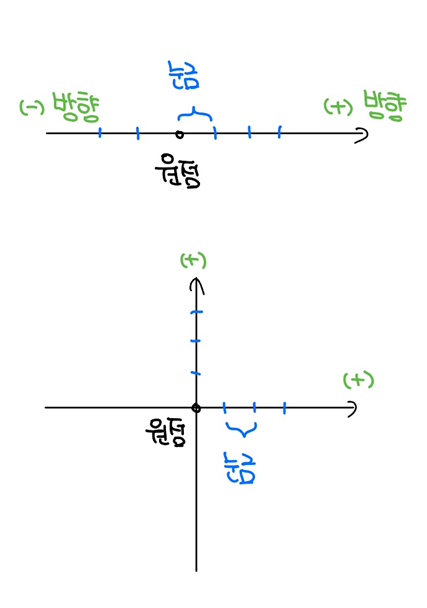
1차원 상에서 reference frame의 (1)원점은 선 위의 적당한 지점(x=0)이 되며, (2)원점의 오른쪽을 (+)방향으로 정한다. 한편 2차원 상에서 frame의 (1)원점은 (x, y)=(0, 0)이 되는 지점으로, (2)원점 위, 오른쪽을 (+)방향으로 정한다.
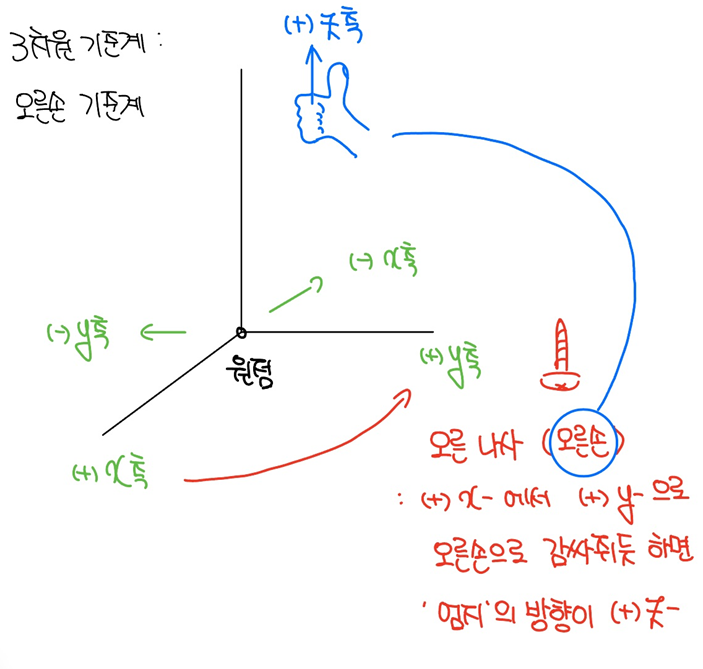
3차원 기준계는 [그림 2]와 같이 오른나사(오른손) 기준계가 많이 쓰이며, (+)축은 각각 (1)지면을 뚫고 나아가는 쪽, (2)오른쪽, 그리고 (3)위쪽이 된다.
좌표계
좌표계란, 특정 공간에 숫자나 기호를 써서 위치를 표기하는 일련의 방식으로 이 때 위치를 지정하는 숫자나 기호는 좌표가 된다.
물리학에서 중점적으로 다루는 좌표계는 2차원에서는 (1)데카르트 좌표계(직각평면좌표계)와 (2)극좌표계이며, 3차원에서는 (1)직각좌표계, (2)원통좌표계, 그리고 (3)구좌표계이다.
2차원 좌표계
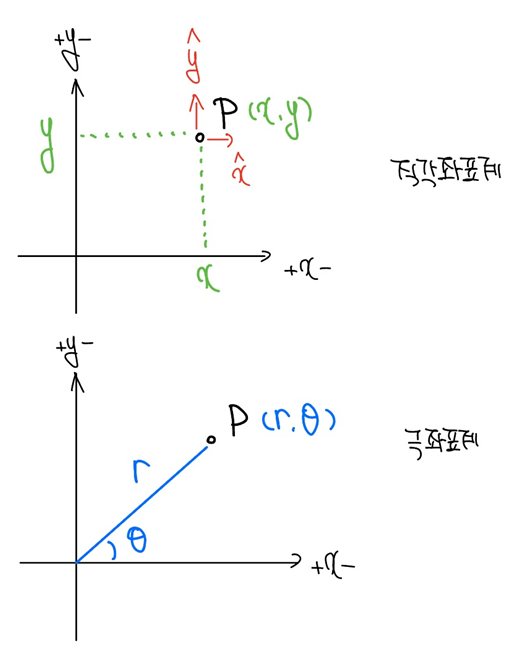
2차원 좌표계는 직각평면좌표계와 극좌표계[그림 3]가 있다.
- 데카르트 좌표계(Cartesian coordinate system): 원점 O(0, 0)을 기준으로 오른쪽 위부터 반시계방향으로 제1, 제2, 제3, 제4사분면으로 나뉘는 좌표계, 임의의 점 P에서 coordinate는 (x, y)로 주어진다.
- 극좌표계(polar coordinate system): 극점(pole) O을 기준으로 (1)pole로부터 떨어진 거리 r과 (2)극점을 지나는 기준선에 대한 각도(반시계 방향) θ로 위치를 표현한다.
3차원 좌표계
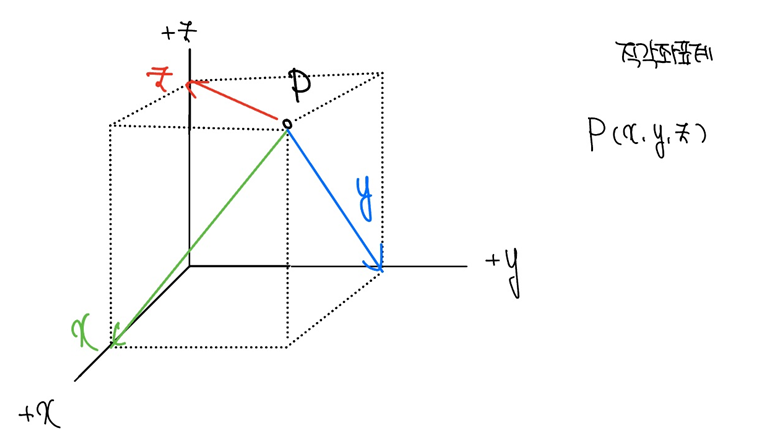
3차원 좌표계의 가장 직관적인 예로 직각좌표계[그림 4]가 있다. 3차원 상에서 coordinate는 (x, y, z)로 주어지며, 상황에 따라 오른손 직각좌표계와 왼손 직각좌표계로 구분되기도 한다.
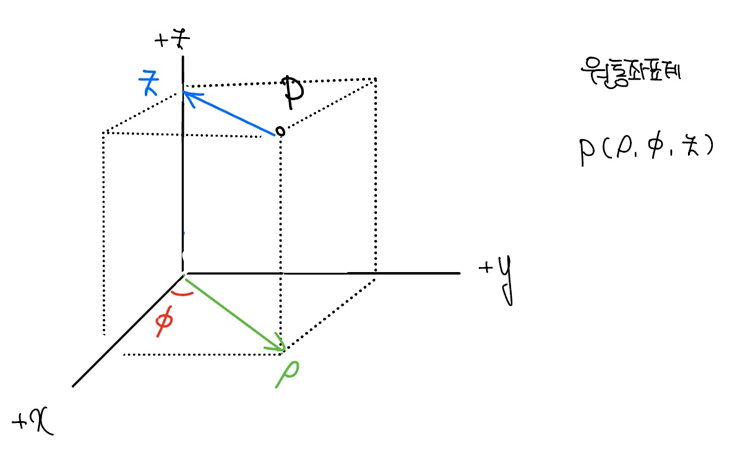
극좌표계에 한 개의 차원을 더 추가하여, z축 방향으로 잡아 늘리면 원통좌표계(cylindrical coordinate)[그림 5]가 된다. polar coordinate system의 r은 원통좌표계의 ρ과 정확히 그 의미가 일치하며, 마찬가지로 세 개의 좌표가 있어야 하기 때문에 P=(ρ, φ, z)로 쓸 수 있다.
- 극좌표계의 세타 θ를 파이로 φ 고쳐쓴다.
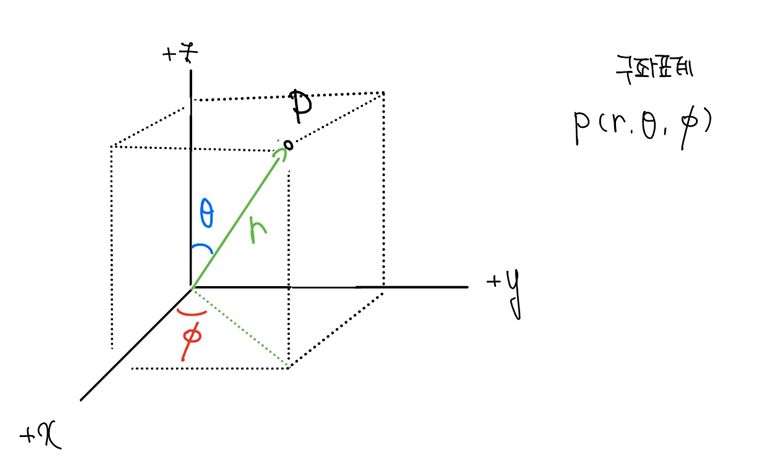
마지막으로 구(면)좌표계(spherical coordinate system)[그림 6]은 (1)원점에서의 거리 r, (2)방위각 θ, (3)천정각 φ를 좌표로 사용하여 위치를 표현한다.
위치벡터, 변위벡터, 속도벡터, 가속도벡터
Position, Displacement, Velocity, and Acceleration Vector
어떤 물질의 움직임을 표현하기 위해서는 4가지의 벡터로 표현되어야 하며, 각각의 정의는 다음과 같다.
- 위치벡터: 기준계의 원점에서 물체가 있는 위치까지 그린 벡터
- 변위벡터: 물체의 처음 위치 r에서 나중 위치 r'까지 그린 벡터
- 속도벡터: 물체가 Δt동안 변위 Δr만큼 이동했을 때의 빠르기 벡터
- 가속도벡터: 물체가 Δt동안 속도 Δv만큼 변했을 때, 시간에 따른 속도의 변화량 벡터

차분과 미분
변위 벡터부터 등장하는 Δ는 나중 값에서 처음 값을 빼라는 의미의 '차분'(difference)이다. 그리고 이 변화량을 순간(양)을 미분(differential)이라 한다.
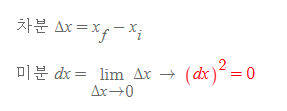
미분 dx의 중요한 성질 중 하나로 dx^2은 0으로 계산된다. ⇒ 무한소 참고
위치벡터와 변위벡터
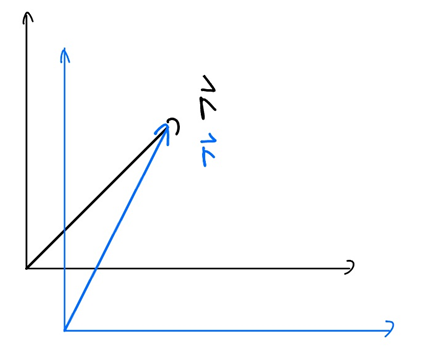
위치벡터는 기준계의 원점으로부터 물체가 있는 위치까지 최단거리로 그은 벡터로 만약 기준계가 [그림 7]과 같이 서로 다르면, 그 크기도 서로 다르다.
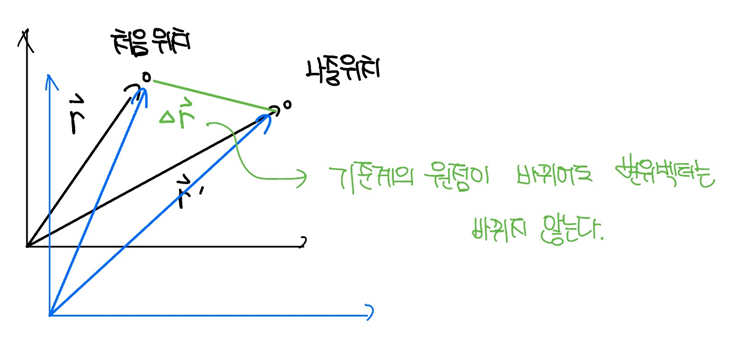
한편 변위벡터는 물체의 나중 위치에서 처음 위치로 벡터차를 한 벡터 값으로 기준계의 원점이 바뀌어도 그 값이 바뀌지 않는 특성[그림 8]이 있다.
평균속도와 순간속도
평균속도는 Δr/Δt로 계산되었다. 그리고 이 차분을 미분으로 바꾸면 '순간속도'(벡터)를 구할 수 있다.
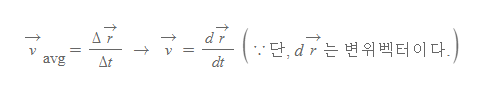
평균가속도와 순간가속도
평균가속도는 Δv/Δt로 계산한다. 그리고 이 차분을 미분으로 바꾸면 '순간가속도'(벡터)를 구할 수 있다.
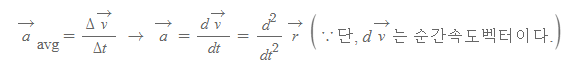
'수학 > 물리학을 위한 수학' 카테고리의 다른 글
| 【물리학을 위한 수학】 05. 벡터미적분학 - 델(나블라) 연산자 (0) | 2025.11.21 |
|---|---|
| 【물리학을 위한 수학】 04. 좌표변환 - 3차원 좌표계 (0) | 2025.11.19 |
| 【물리학을 위한 수학】 03. 원운동 해석 (0) | 2025.11.18 |
| 【물리학을 위한 수학】 02. 좌표변환 - 2차원 좌표계 (0) | 2025.11.17 |
| 【미분방정식】 Chapter 1. 변수분리형 방정식 (0) | 2024.10.28 |





