Herald-Lab
【물리학을 위한 수학】 03. 원운동 해석 본문

2차원 평면좌표계로 우리는 (1)직각좌표계와 (2)극좌표계를 배웠다. 특히 극좌표계는 물체가 2차원 평면에서 원을 그리는 원운동(圓運動, circular motion)을 해석하는 데 매우 유용하다. 원운동 중 등속원운동(uniform circular motion)을 극좌표계를 활용하여 해석해보자.
등속원운동(等速圓運動)
Uniform Circular Motion
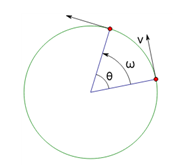
질점(point particle)으로 표현되는 물체가 일정한 속력 v로 원을 그리는 운동을 등속원운동이라 하며, 일상에서 매우 흔하게 발견된다. 등속원운동은 속력 v는 일정하지만 x좌표와 y좌표는 계속 변하기 때문에 속도는 항상 변한다. 또한 등속원운동하는 물체와 원의 중심 사이 거리 r은 항상 일정하다.
- 속력 v는 항상 일정하다.
- 물체와 원의 중심 사이 거리 r은 항상 일정하다.
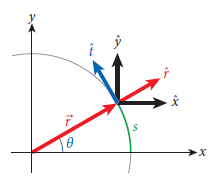
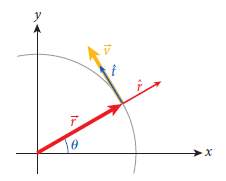
원운동을 하는 동안 물체의 x, y좌표는 항상 변하고 이러한 특성을 극좌표(polar coordinates)로 다룰 수 있다. [그림 1]의 벡터 r은 원운동을 하는 물체의 위치벡터를 나타낸다.
- r: 벡터 r의 길이
- θ: x축에 대한 벡터의 각도
데카르트 좌표를 활용해 극좌표를 변환하면 다음과 같다.
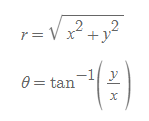
반대로 극좌표를 데카르트 좌표로 바꾸면 아래와 같다.
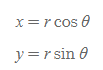
polar coordinates의 두 값은 위와 같이 r과 θ로 나타낼 수 있으며, 이들의 단위벡터 또한 (1)반지름 방향 단위벡터 r과 (2)접선 방향 단위벡터 t(단위벡터 θ)로 표현할 수 있다.
- 반지름 방향 단위벡터 r: radial unit vector, θ는 일정하게 유지한 채 r만 증가하는 방향
- 접선 방향 단위벡터 t: tangential unit vector, 원운동하는 입자의 접선방향으로 r은 일정하게 유지한 채 θ만 증가한다.
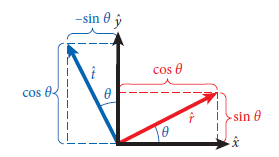
[그림 2]와 같이 radial과 tangential 단위벡터 사이에는 일정한 θ 값이 있고 이를 삼각함수로 표현하면 다음과 같다.
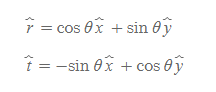
radial과 tangential이 서로 수직함은 dot product의 결과 값으로 증명할 수 있다.
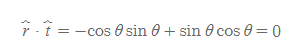
원운동에서 극좌표 단위벡터는 시간에 따라 방향이 변한다. 그 이유는 radial 단위벡터와 tangential 단위벡터는 θ에 의존하고, 등속원운동에서 θ는 시간에 따라 항상 변하기 때문이다.
원운동의 각속도와 선속도
Angular Velocity and Linear Velocity
2차원 평면상에서 원운동하는 물체의 위치벡터 r을 시간에 대해 미분하면 선속도[그림 3]를 구할 수 있다.
위치벡터
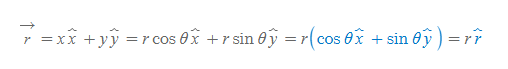
선속도벡터
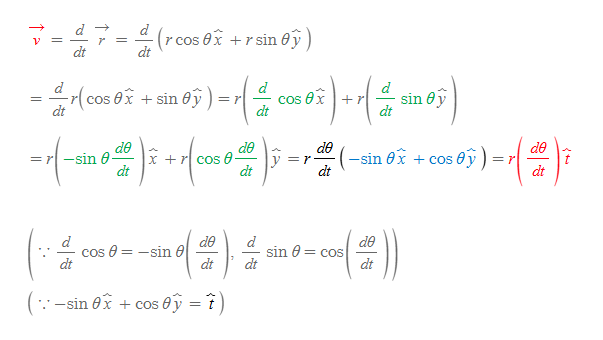
선속도벡터 식에서 dθ/dt는 각속도(angular velocity)로 시간 t에 따른 물체의 이동각 θ을 뜻하며, ω(omega)[그림 4]로 쓴다.
원운동하는 물체의 각속도
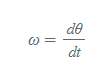
■
원운동하는 물체의 선속도
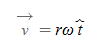
■
선속도 벡터는 tangential 단위벡터가 사용된다. 즉, 선속도 벡터는 원운동의 접선 방향[그림 3]으로 나타난다.
<물리량>
- r: 등속 원운동하는 물체와 원의 중심 사이 거리
- ω: 물체의 각속도
- hat t: tangential 단위벡터
선속도의 크기만 따지면 식은 다음과 같이 간단해진다.
선속도 크기
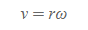
■
등속원운동에서 각속도는 회전축을 방향을 선속도는 접선방향을 가리킨다.
각가속도와 선가속도
Angular Acceleration, and Linear Acceleration
각가속도란, 각속도의 변화율이며 그 값은 아래와 같이 정의한다.
(순간) 각가속도
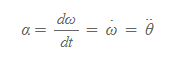
■
선가속도는 선속도의 시간에 대한 미분 값으로, 아래와 같이 식을 풀어 쓸 수 있다.
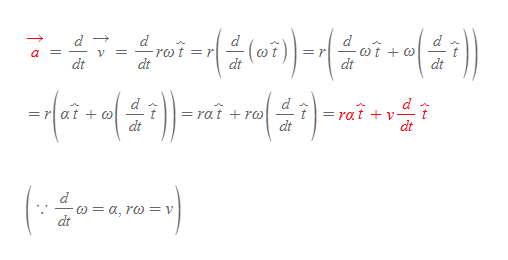
선가속도
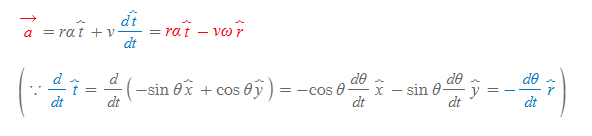
■
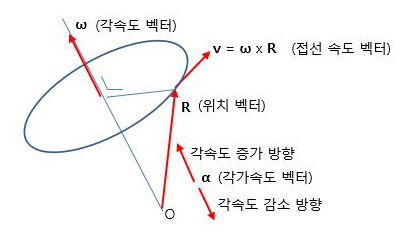
각속도, 선속도, 각가속도 등은 모두 벡터 물리량으로 [그림 5]와 같이 방향성이 나타난다.
'수학 > 물리학을 위한 수학' 카테고리의 다른 글
| 【물리학을 위한 수학】 05. 벡터미적분학 - 델(나블라) 연산자 (0) | 2025.11.21 |
|---|---|
| 【물리학을 위한 수학】 04. 좌표변환 - 3차원 좌표계 (0) | 2025.11.19 |
| 【물리학을 위한 수학】 02. 좌표변환 - 2차원 좌표계 (0) | 2025.11.17 |
| 【물리학을 위한 수학】 01. 기준계와 좌표계 (0) | 2025.11.16 |
| 【미분방정식】 Chapter 1. 변수분리형 방정식 (0) | 2024.10.28 |





