Herald-Lab
【물리학을 위한 수학】 04. 좌표변환 - 3차원 좌표계 본문

각 차원 좌표계에서 단위벡터를 활용해 (1)위치벡터, (2)변위벡터, (3)속도벡터, (4)가속도벡터를 구했다. 마찬가지로 세 가지의 3차원 좌표계에서도 같은 벡터량들을 구할 수 있다.
- 직교좌표계
- 원통좌표계
- 구좌표계
직교좌표계
Cartesian Coordinate System
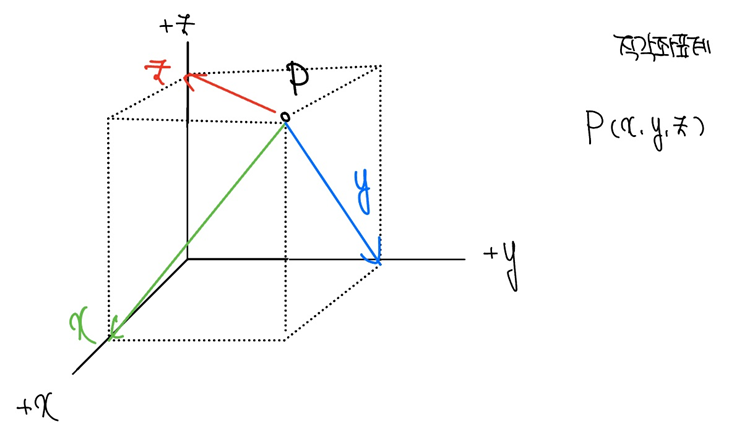
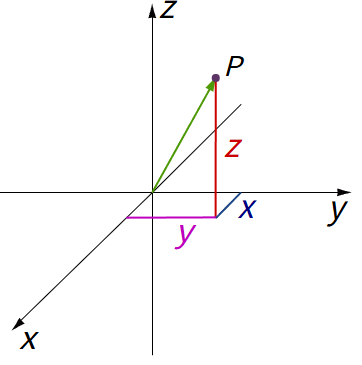
3차원의 Cartesian 좌표계는 [그림 1]과 같이 특정한 P점에 대해 (x, y, z) 좌표 값을 갖는다.
직교좌표계의 벡터 값은 다음과 같다.
직교좌표계 벡터량

■
원통좌표계
Cylindrical Coordinate System
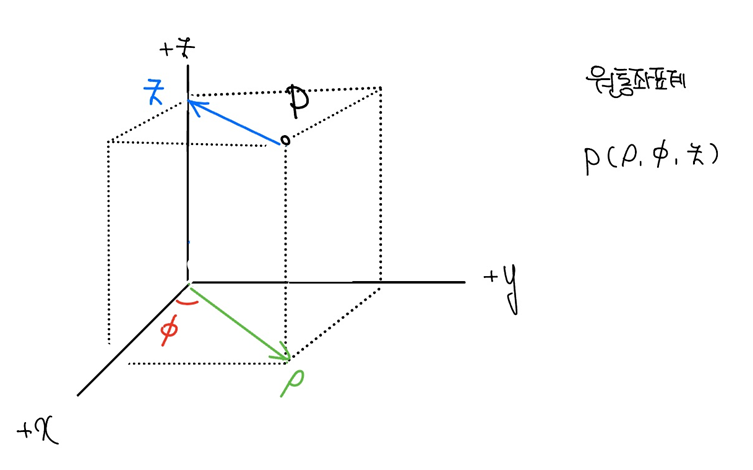
원통좌표계[그림 2]는 2차원 극좌표계의 확장형으로, 수식적으로는 Cartesian 좌표계와 spherical 좌표계의 중간 지점에 있다.
원통좌표계의 3가지 좌표 의미는 아래와 같다.
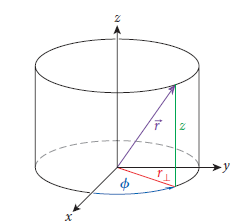
- ρ: 또는 [그림 3]의 r⊥, xy평면으로 투영했을 때의 반지름
- φ: xy평면상의 방위각(azimuthal angle)
- z: Cartesian coordinate system의 z와 같은 값
원통좌표계의 벡터량은 극좌표계의 같은 내용에 z항을 추가한 것과 같다. 우선 극좌표계의 벡터량은 아래와 같이 구하였다.
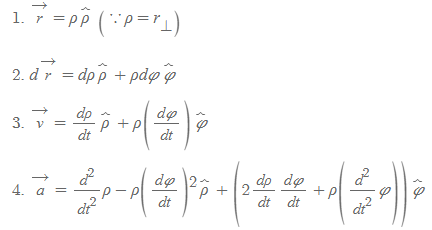
이 극좌표계 벡터량에 z항을 추가하면 다음과 같이 벡터량 식을 정리할 수 있다.
원통좌표계 벡터량
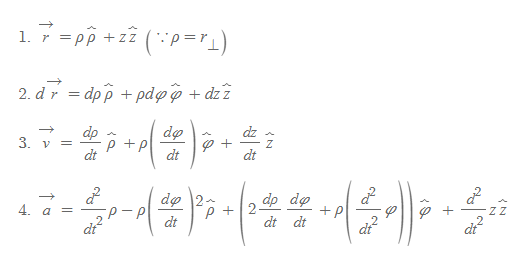
■
또한 단위변환의 측면에 있어서, Cartesian과 cylindrical은 아래와 같이 항이 변화한다.
Cartesian을 활용한 원통좌표
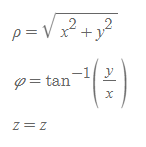
원통좌표를 활용한 Cartesian
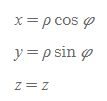
구좌표계
Spherical Coordinate System
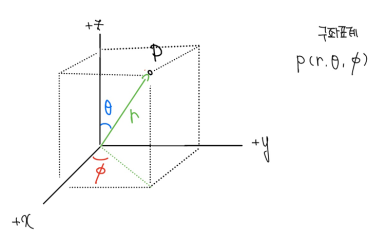
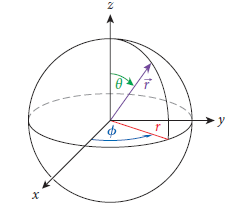
구좌표계 또는 구면좌표계는 위치벡터 r의 집합이 구면을 형성하는 좌표계로 3가지 좌표는 아래와 같다.
- r: 원점으로부터의 거리
- θ: 양의 z축으로부터 내려오는 극각(polar angle)
- φ: xy평면 위의 투영 벡터가 x축과 이루는 방위각(azimuthal angle) ⇒ 원통좌표계의 방위각과 정확히 일치
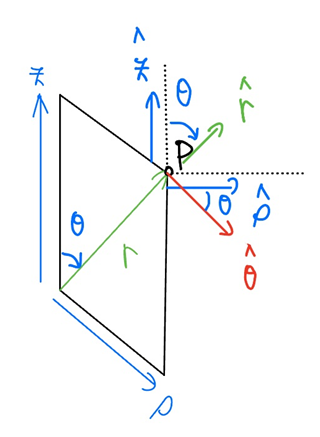
구좌표계에서의 벡터량들을 구하기 위해, [그림 5]의 정보를 활용하여 원통좌표계와 구좌표계의 단위벡터들을 직교좌표계 단위벡터로 표현해야 한다.
원통좌표계 단위벡터 변환
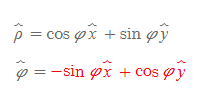
구좌표계 단위벡터 표현
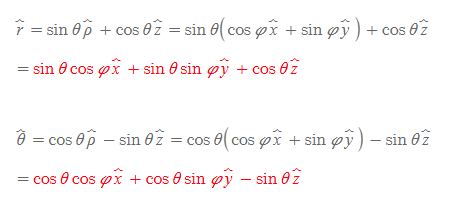
위의 내용을 종합하면 구좌표계의 단위벡터들을 직교좌표계 단위벡터로 변환하여 표현할 수 있다.
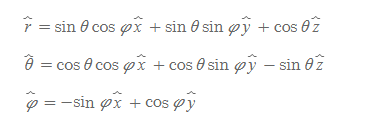
이들 단위벡터를 미분하면 다음과 같이 계산된다.
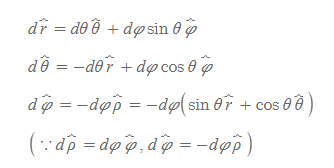
위의 단위벡터와 그 미분값들을 통해 아래 벡터량을 구할 수 있다.
구좌표계 벡터량
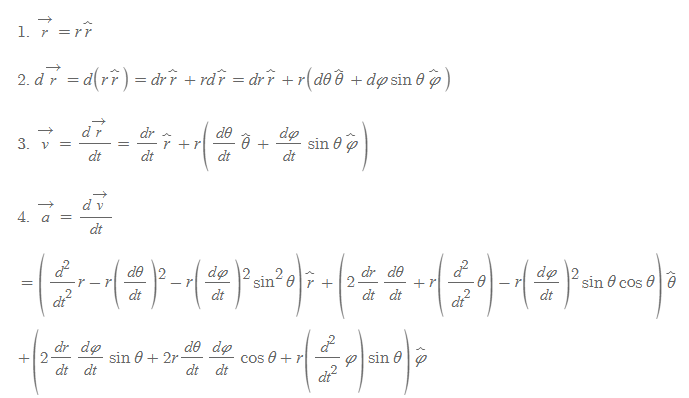
■
원통좌표계와 마찬가지로 구면좌표계 또한 Cartesian을 활용하여 그 값을 변환할 수 있다.
Cartesian을 활용한 구좌표
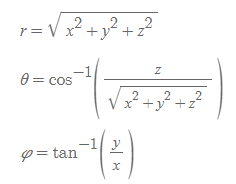
구좌표를 활용한 Cartesian
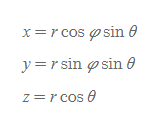
'수학 > 물리학을 위한 수학' 카테고리의 다른 글
| 【물리학을 위한 수학】 06. 벡터미적분학 - 그래디언트(Gradient) (0) | 2025.11.22 |
|---|---|
| 【물리학을 위한 수학】 05. 벡터미적분학 - 델(나블라) 연산자 (0) | 2025.11.21 |
| 【물리학을 위한 수학】 03. 원운동 해석 (0) | 2025.11.18 |
| 【물리학을 위한 수학】 02. 좌표변환 - 2차원 좌표계 (0) | 2025.11.17 |
| 【물리학을 위한 수학】 01. 기준계와 좌표계 (0) | 2025.11.16 |





