Herald-Lab
【물리학을 위한 수학】 06. 벡터미적분학 - 그래디언트(Gradient) 본문

물리학에서의 많은 물리량은 벡터량으로 분류되고, 그 공식들은 벡터함수의 꼴을 갖는다. 벡터 미적분학은 2차원 이상의 다변수 실해석과 관련한 미적분학의 한 분야로 벡터장 모델을 구현 및 해석하는 데 필수적이다.
- 함수: 두 변수 x, y 사이에서 독립변수 x의 값에 따라 종속변수 y의 값이 정해지면, y는 x의 함수라 하고 y=f(x)라 쓴다.
- 장(場, field): 마당, 필드, 3차원 공간계를 예로 들면, 어떤 함수 중 독립변수가 공간의 위치인 좌표 x, y, z를 갖는 함수, 함수 중에서 독립변수가 공간의 위치인 coordinate이면, 그 함수를 field라 한다.
스칼라장과 벡터장
Scalar Field and Vector Field
스칼라장
스칼라장(scalar field)이란, 특정한 공간 속의 각 점에 대해 스칼라량을 대응시킨 공간장을 뜻한다. 예를 들어 온도 분포가 존재하는 방을 생각할 때, 특정한 지점에서의 온도 T는 명백히 위치에 따른 함수임을 알 수 있다. 각 지점에 대한 온도 scalar를 x, y, z로 대응한다.

일반적으로 스칼라장은 φ로 적으며, 각 지점에 대해 숫자가 대응되는 공간장을 아래와 같이 표현한다.
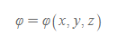
물리학에서 스칼라장[그림 1]은 대표적으로 온도 분포, 수압 분포, 전위 분포, 퍼텐셜에너지 분포 등이 있다.
- 스칼라장에서 각 점은 gradient를 갖는다.
벡터장
벡터장(vector field)은 특정한 공간 속의 각 점에 대해 벡터량을 대응시킨 공간장을 뜻한다. 벡터장의 공간위치는 벡터량이다.
- 벡터장의 공간위치는 '위치벡터'를 들 수 있다.
일반적으로 벡터장은 v로 적으며, 벡터장 함수는 아래와 같이 표현한다.

- 벡터공간의 각 점에 위의 벡터가 대응된다.
- 복소평면에서의 2차원 벡터장 또한 표현가능하다.
물리학에서 벡터장은 대표적으로 중력장, 전기장, 그리고 자기장 등이 있다.
그래디언트
Gradient
scalar function f를 f=f(x, y, z)라고 표현했을 때, del operator를 사용한 아래 식을 f의 그래디언트(gradient)라고 정의한다.
Gradient
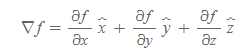
■
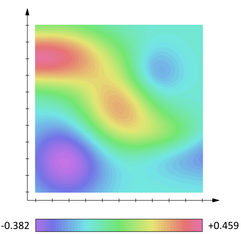
gradient는 벡터량으로 스칼라장의 최대 증가율을 나타낸다.

gradient는 scalar field에서 화살표[그림 2]로 나타난다. (1)화살표의 방향은 증가율이 최대가 되는 쪽이며, (2)화살표의 크기는 증가율의 크기를 뜻한다.
예를 들어 온도장의 그래디언트란 온도의 증가율이 가장 큰 방향을 가리키는 벡터이다.

위 식에서 온도장은 scalar field인 φ(x, y, z)로 표현했다.
원통좌표계와 구좌표계의 Gradient
위에서 살펴본 gradient의 기본식은 직교좌표계에서 유효하다. 그러나 ∇값은 원통좌표계와 구좌표계에서 아래와 같이 변한다.
- 원통좌표계 del operator

- 구좌표계 del operator

따라서 두 좌표계에서의 gradient 값 또한 아래와 같이 고쳐써야 한다.
Gradient(원통좌표계)

■
Gradient(구좌표계)
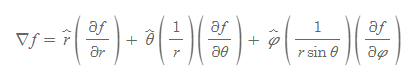
■
gradient의 식은 간단하게 grad φ라고도 쓸 수 있다.
그래디언트의 활용: 보존력
Applications of Gradient: Conservative Forces
물리학에서 보존력(保存力, conservative force)이란, 어떤 물체가 지점 A에서 지점 B로 이동할 때 경로(path)에 상관없이 오직 시작점과 끝점만으로 '일(work)'이 결정되는 힘을 뜻한다.
- 보존력에 의해 한 점에서 다른 점으로 이동할 때의 일은 경로에 무관하다.
보존력(F)이 한 일(work)과 퍼텐셜 에너지의 관계는 다음과 같다.
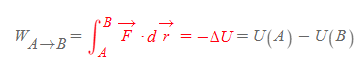
위의 식에서 (1)퍼텐셜에너지가 가장 작은 지점 U_A 지점을 0으로 잡고 (2)보존력 F를 중심으로 정리하면, 보존력의 정의를 구할 수 있다.

보존력

■
3차원에서 보존력은 퍼텐셜에너지의 음의 gradient이고, 힘이기 때문에 벡터량이다.
- 보존력은 항상 계가 가질 수 있는 가장 작은 퍼텐셜에너지를 갖도록 작용한다.
- 보존력 식에서 음수부호는 가장 작은 위치에너지 값을 갖도록 만드는 보존력의 특성을 반영한다.
'수학 > 물리학을 위한 수학' 카테고리의 다른 글
| 【물리학을 위한 수학】 08. 벡터미적분학 - 다이버전스(Divergence) <PART 2> (0) | 2025.11.25 |
|---|---|
| 【물리학을 위한 수학】 07. 벡터미적분학 - 다이버전스(Divergence) <PART 1> (0) | 2025.11.23 |
| 【물리학을 위한 수학】 05. 벡터미적분학 - 델(나블라) 연산자 (0) | 2025.11.21 |
| 【물리학을 위한 수학】 04. 좌표변환 - 3차원 좌표계 (0) | 2025.11.19 |
| 【물리학을 위한 수학】 03. 원운동 해석 (0) | 2025.11.18 |





