Herald-Lab
【물리학을 위한 수학】 08. 벡터미적분학 - 다이버전스(Divergence) <PART 2> 본문

벡터미적분의 divergence 개념은 물리학의 전반에서 system의 한 지점으로부터 벡터장이 퍼지는 지(발산) 아니면 모여서 사라지는 지(수렴)를 보여주는[그림 1] 중요한 물리량이다.
- 직교좌표계에서 divergence는 임의의 한 점(x, y, z)에 있는 공간 내에 벡터장이 퍼지는 지 아니면 모여서 사라지는 지를 나타낸다. ⇒ 벡터장이 사방으로 뻗어나가면 0보다 큰 값, 벡터장이 사방에서 어느 한 지점으로 빨려들어간다면 0보다 작은 값, 마지막으로 들어오는 양과 나가는 양이 동일하면 0이다.
- 벡터장의 divergence는 각 점에서의 스칼라 값으로 나타난다.
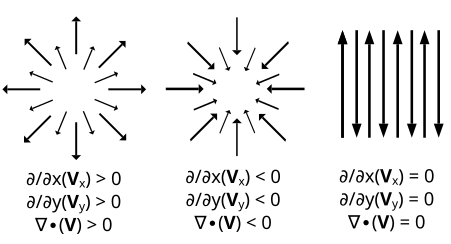
divergence는 주어진 한 지점에서 벡터장의 선속(flux) 경향을 수치적으로 나타낸 지표로 (1)발산(divergence), (2)소멸(sink), (3)무원천(no source)의 세 형태[그림 2]로 나타난다.
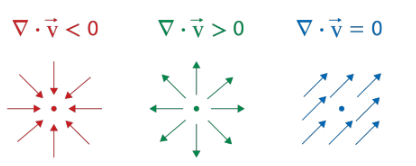
- 다이버전스의 결과가 양수이면, 한 지점에서 스칼라는 발산한다.
- 다이버전스의 결과가 음수이면, 한 지점에서 스칼라는 소멸한다.
- 다이버전스의 결과가 0이면, 한 지점에서 스칼라의 변화는 없으며, 이는 곧 장을 변화시키는 원천이 없다는 뜻이다.
직교좌표 x, y, z에 대해 v(x, y, z)를 미분가능한 벡터함수라고 하고, v의 각 성분을 v_x, v_y, v_z라 둘 때, divergence는 다음과 같이 정의한다.
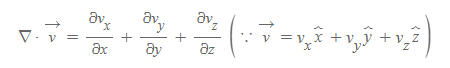
발산량에 관하여
About the Value of Divergence
어떠한 벡터장에서의 발산량을 구하기 위해서 두 가지의 특징을 기억하도록 한다.
- divergence는 공간상의 변화'만' 고려한다. 시간에 따른 변화는 고려하지 않는다.
- divergence는 미소영역 내에서의 '무수한 입자'들의 밀도 변화를 뜻한다.
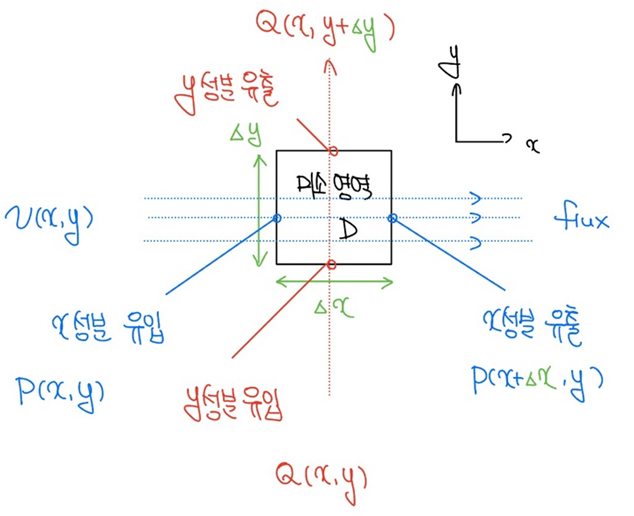
입자의 밀도란, 그 입자가 어떤 차원을 어떤 식으로 움직이느냐에 따라 그 식이 약간씩 달라지는데, [그림 3]과 같이 평면상에 1차원적으로만(x축 또는 y축 이동만) 움직이면, 밀도 식에서 부피는 길이로 바뀐다.
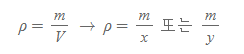
다음, 계산을 쉽게 하기 위해 벡터장 v를 2차원이라 가정하고, 이때의 발산량을 [그림 3]과 같이 미소영역에 대해 구해보자.
[1] 우선 벡터장 v를 아래와 같이 표현한다.
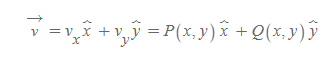
여기서 P와 Q는 각각 x축과 y축에서의 벡터 v의 크기를 나타낸다.
[2] 미소영역에서 발산량은 같은 영역에서의 flux 내 무수한 입자들의 밀도 변화로 유입과 유출로 판단한다.
- 각 좌표축에서의 발산량 = (유출량 - 유입량)/Δx or (유출량 - 유입량)/Δy
[3] x축의 발산량
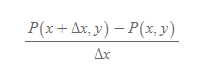
[4] y축의 발산량
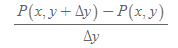
[5] [과정 3]과 [과정 4]에서 유도된 발산량은 미소 영역에서의 각 축에 대한 길이를 특정한 값으로 극한 값을 취해주면 아래와 같이 계산된다.
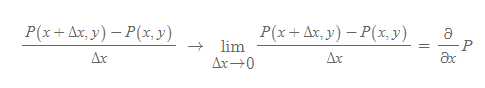
y에 대해서도 똑같이 극한을 취해주면,
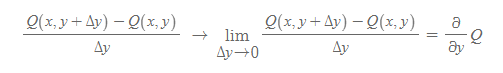
이다.
각각의 극한은 x에 대한 편미분, y에 대한 편미분으로 표현된다.
[6] 미소영역에서의 전체 변화는 [과정 5]의 편미분 값의 합과 같다.
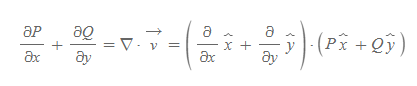
'수학 > 물리학을 위한 수학' 카테고리의 다른 글
| 【물리학을 위한 수학】 10. 벡터미적분학 - 컬(회전) <PART 1> (0) | 2025.12.01 |
|---|---|
| 【물리학을 위한 수학】 09. 벡터미적분학 - 발산 정리 (0) | 2025.11.29 |
| 【물리학을 위한 수학】 07. 벡터미적분학 - 다이버전스(Divergence) <PART 1> (0) | 2025.11.23 |
| 【물리학을 위한 수학】 06. 벡터미적분학 - 그래디언트(Gradient) (0) | 2025.11.22 |
| 【물리학을 위한 수학】 05. 벡터미적분학 - 델(나블라) 연산자 (0) | 2025.11.21 |





