Herald-Lab
【물리학을 위한 수학】 09. 벡터미적분학 - 발산 정리 본문

발산 정리(發散 定理, divergence theorem): 벡터장 선속(flux)는 그 발산의 삼중적분과 같다
- 폐곡면 위의 면적분을 계산할 때 매우 유용하다.
벡터장선과 벡터선속
Vector Field Line and Flux
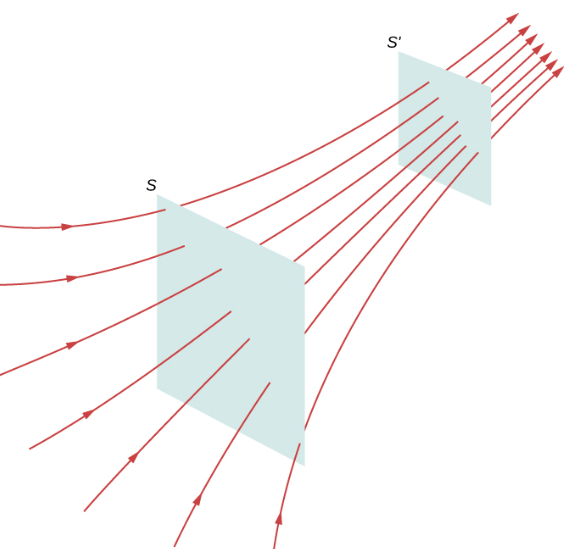
벡터장선(vector field line): 벡터장에 그려진 개별적인 선, [그림 1]의 빨간 선
- 모든 벡터는 벡터장선의 형태로 표현 가능하다.
- 어떤 위치에서 벡터장의 방향은 그 위치에서의 벡터장선의 접선방향과 같다.
- 어떤 위치에서 벡터장의 크기는 그 위치(면적)에서의 flux에 비례[그림 2]한다.
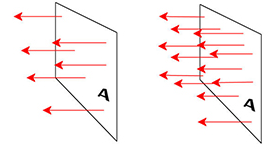
벡터선속(vector field flux): 벡터장 선속, 또는 선속(flux), 벡터장에 놓은 면을 지나는 벡터장선의 개수에 비례하는 양, 임의의 면적 S에 대한 다발(bundle) 형태로 그려진다.
- 선속(線束, flux): 특정한 면적을 통과하는 특정한 물리량의 흐름 ⇒ 특정 물리량이 되는 대상은 전기장, 자기장, 유체, 열 등 흐름의 형태[그림 3]를 갖는다.

벡터장의 크기를 F라 두었을 때, F는 그 위치에서의 flux에 비례한다고 하였다. 즉, 특정 면에 대한 흐름의 밀도 관점에서, 벡터장은 [그림 1]과 같이 벡터장에 놓인 면 S에 대해 'S당 지나는 flux의 크기'라 정의할 수 있다.
벡터장
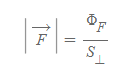
■
<물리량>
- F: 벡터장
- Φ: 벡터장선의 개수
- S_⊥: 벡터장선에 수직한 면의 면적(area)
Flux
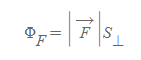
■
벡터장은 면에 대해서는 그 방향에 수직(⊥)할 때, 면벡터에 대해서는 그 방향이 평행할 때 가장 큰 값을 갖는다.
면에서의 법선벡터(면벡터)
Normal Vector on a Surface
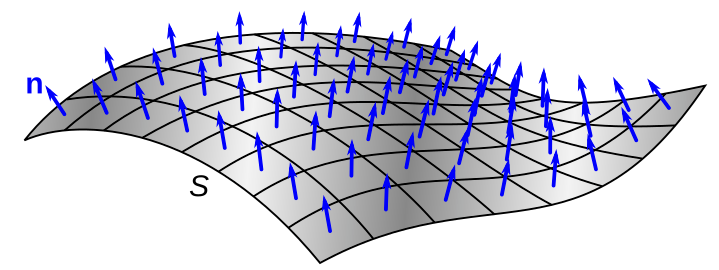
[그림 4]와 같이 어떤 가상의 면이 있다고 할 때 면이 갖는 법선벡터(normal vector)는 국소적인 영역 S에 대해 파란색 화살표와 같이 나타낸다. 이 normal vector의 크기와 방향은 다음과 같다.
- 크기: 면의 넓이
- 방향: 면에 수직한 방향
특히 면에 수직한 방향은 단위벡터 개념을 활용하여 [그림 5]와 같이 hat n으로 표현한다.
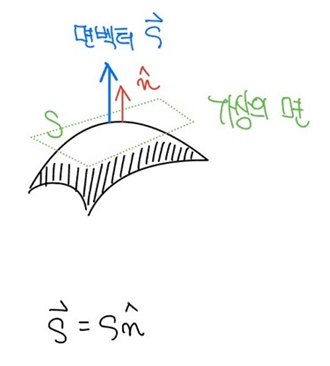
따라서 면벡터의 식을 다음과 같이 쓸 수 있다.
면벡터
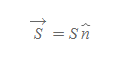
■
벡터장의 최댓값
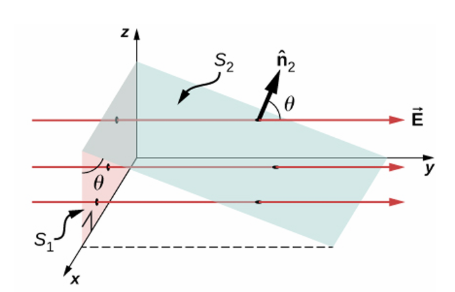
벡터장의 한 가지 예로 전기장 E가 [그림 6]와 같이 지나갈 때 임의의 파란색 면을 경사지게 설정하면, 전기장 E와 수직하지는 않지만, 비스듬한 각도 θ를 두고 단위벡터 n_2를 지정할 수 있다. 벡터장은 면벡터에 대해서 평행할 때 가장 큰 값을 갖는데, 비스듬한 각도를 두고 다음과 같은 관계식을 쓸 수 있다.
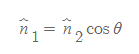
여기서 단위벡터 n_1은 벡터장의 크기가 항상 최대값인 벡터장과 평행한 단위벡터를 뜻한다.
면적소에서의 벡터장 선속

임의의 면에 대해 [그림 7]과 같이 면적소(area element)를 나누었을 때, 이 면을 통과하는 flux는 벡터장의 크기 식을 통해 아래와 같이 구할 수 있다.
- 면적소: 임의의 면에 대한 국소지역의 면적
면적소 Flux
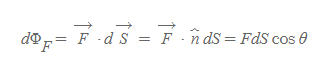
■
벡터장의 최댓값에서 다룬 단위벡터의 관계식을 활용해 flux를 벡터장과 면벡터의 내적한 값으로 정의할 수 있다. 또한 비록 균일하지 않은 벡터장이라도, 면을 매우 잘게 나누면, 그 미분된 면에 한하여서는 벡터장이 균일하다고 가정할 수 있다.
면적소 dS를 통과하는 벡터장 선속을 위와 같이 쓸 수 있는데, 이를 전체 면적으로 확장하면 면적분(surface integral)을 해주면 된다.
면 Flux
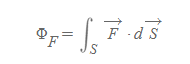
■
즉, 면에 대한 flux는 flux를 감싼 표면의 형태에 의해 결정된다.
발산 정리
Divergence Theorem
위의 사고 과정을 통해 우리는 (1)flux가 벡터장과 면벡터의 내적이고, 이들 전체 값은 (2)(폐)곡면의 적분임을 확인했다.
- 폐곡면: 면의 가장가지가 모두 연결된 면
그리고 이 flux는 divergence의 부피적분 값과도 같은데, 아래에서 이를 증명하겠다.
발산 정리
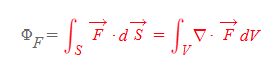
■
발산정리의 증명
[그림 8]과 같이 여덟 개의 정육면체가 쌓여있다고 할 때 유체의 흐름은 (1)서로 육면체가 마주하지 않는 면에서는 통과, (2)안쪽끼리 맞닿은 면에서는 상쇄된다. 따라서 표면적에 대해서 flux를 모두 구하면 다음과 같다.
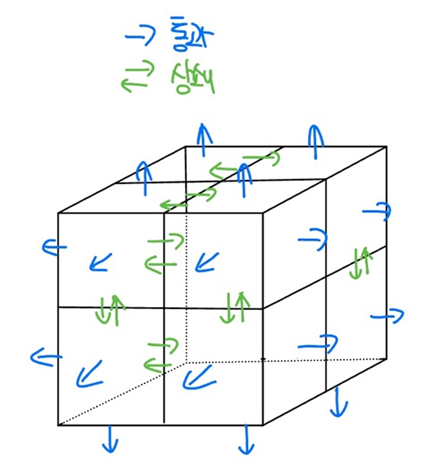
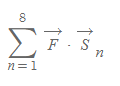
위는 8개의 정육면체가 갖는 면에 대해 모두 flux를 계산하는 식이다. 이때 8개의 정육면체를 미지수 n의 개수로 무한히 늘리면 아래와 같이 식이 변한다.
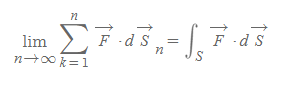
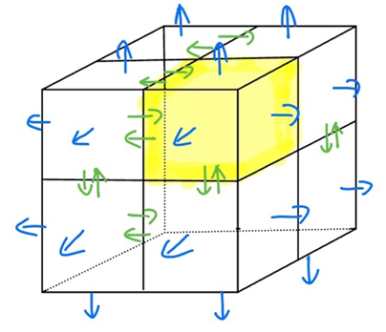
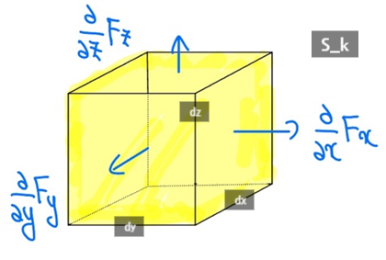
시그마 내부의 항은 어떠한 미소부피로부터 빠져나간 유량으로 [그림 9]와 같이 x, y, z축으로 알짜유량이 존재하는 부피소(volume element) S_k를 모두 더하는 식으로 전체 flux를 구할 수 있다.
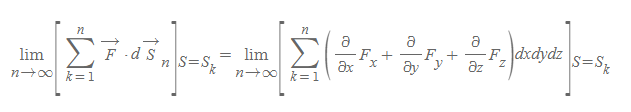
위의 두번째 식에서 두 가지 값을 고쳐쓸 수 있다.
- 부피소의 미소길이 dx, dy, dz를 모두 곱하면 미소부피 dV가 된다.
- 괄호 안 편미분 항은 직교좌표계의 divergence 값이다.
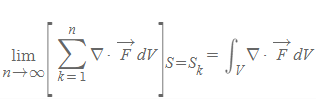
'수학 > 물리학을 위한 수학' 카테고리의 다른 글
| 【물리학을 위한 수학】 11. 벡터미적분학 - 컬(회전) <PART 2> (0) | 2025.12.05 |
|---|---|
| 【물리학을 위한 수학】 10. 벡터미적분학 - 컬(회전) <PART 1> (0) | 2025.12.01 |
| 【물리학을 위한 수학】 08. 벡터미적분학 - 다이버전스(Divergence) <PART 2> (0) | 2025.11.25 |
| 【물리학을 위한 수학】 07. 벡터미적분학 - 다이버전스(Divergence) <PART 1> (0) | 2025.11.23 |
| 【물리학을 위한 수학】 06. 벡터미적분학 - 그래디언트(Gradient) (0) | 2025.11.22 |





