Herald-Lab
【물리학을 위한 수학】 11. 벡터미적분학 - 컬(회전) <PART 2> 본문

이전 챕터에서 벡터장 F에 대해 curl은 각 지점에서 벡터장이 얼마나 회전하고 있는지, 회전의 세기와 회전축의 방향을 표현한다고 배웠다. curl은 3차원의 좌표계에서 각각 아래와 같이 표현된다. (단, 이 식의 유도는 단위벡터의 벡터 외적을 사용하여 직접 해보도록 하자.)
직교좌표계 Curl

■
원통좌표계 Curl

■
구좌표계 Curl

■
물리학적으로 curl의 직관적 이미지는 (1)크기와 (2)방향을 들 수 있다.
1. 컬의 방향: 오른쪽 법칙을 따르며, 벡터장의 회전 방향이 손가락이 감기는 방향이라면, 엄지가 가리키는 방향이 curl의 방향[그림 1]이다.
2. 컬의 크기: 벡터장이 한 점을 중심으로 얼마나 강하게 회전하는 지 나타내는 요소로, 회전이 강할 수록 curl의 크기가 커진다.
- curl이 0이라면, 벡터장은 그 점의 주변에서 회전이 발견되지 않는다. ⇒ 보존장(conservative field)의 정의

컬의 유도(2차원 평면)
직교좌표계를 기준으로 curl 공식을 유도하기 위해서는 다음 내용을 우선 알아야 한다.
- curl은 벡터장에서의 넓이의 회전이 아닌 [그림 2]와 같은 테두리 상에서의 회전이다.
- curl은 거시적인 장이 아닌 미시적인 수준에서의 회전을 나타낸다. ⇒ 편미분을 취하는 근거
위의 두 가지 사항에 대해 알아보았으면, 다음 벡터장 F(F=P(x, y)x^+Q(x, y)y^)를 아래와 같이 가정하자.

- [그림 2]와 같이 벡터장에서의 curl은 임의의 정사각형(2Δx × 2Δy)의 테두리에서 발생하고, 이때 Δx, Δy는 매우 작다.
- curl의 회전 방향은 반시계 방향일 때 (+), 시계 방향일 때 (-) 부호를 취한다.
- 임의의 사각형 테두리에 대한 x-축, y-축 (+)방향은 [그림 2]의 오른쪽 상단에 제시되었다.

위의 테두리에 [그림 3]과 같이 막대기가 놓여져 있다고 하자. [그림 3]의 첫 번째 그림은 막대가 x축으로 놓인 것이고, 두 번째는 막대가 y축으로 놓인 것이다. 각 지점 1, 2, 3, 4는 막대의 중심을 (0, 0)이라 했을 때 위와 같이 쓸 수 있다.
[그림 3] 해석

[그림 3]의 첫 번째 상황에서 x축에 놓인 막대가 반시계 방향으로 돌기 위해서는 연두색 화살표 방향으로 힘이 작용해야 하며, 주어진 벡터장의 테두리에서는 2개의 연두색 화살표로 표현된다. ⇒ 회전시키는 힘을 계산하기 위해 2Δx의 길이를 가진 막대기에 대해(당) 두 개의 연두색 벡터값을 합(+)한다.
그리고 이 지점([그림 3]의 1번, 2번)에서의 벡터장은 P, Q 파란색 화살표의 합(빨간색 화살표)으로 표현된다.

위 두 식에서 막대기가 회전하기 위한 유효 방향은 y축'만'이므로 식의 Q항만 살아남는다.

[그림 4] 지점의 curl은 2Δx의 길이 당 두 개의 힘을 더한 값이다.
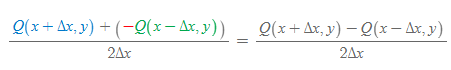
- 단, Q(x-Δx, y)y^는 임의의 사각형 테두리에 대한 y축에 대해 (-)방향성을 띠고 있으므로, 위 식에서 (-1)을 곱한 빨간 부호로 나타난다.
그리고 위 벡터장 테두리는 미소 영역이기 때문에 극한 후 편미분으로 표현할 수 있다.


같은 방식으로 막대가 세로로 놓여있을 때 반시계 방향 curl은 [그림 5]의 내용과 같이 전개된다.

회전의 정방향을 시계 반대 방향이라 [그림 3]의 1, 2, 3, 4 지점에서의 총합 및 방향을 다음과 같이 쓸 수 있다.

'수학 > 물리학을 위한 수학' 카테고리의 다른 글
| 【물리학을 위한 수학】 13. 변수분리형 미분방정식 (0) | 2025.12.27 |
|---|---|
| 【물리학을 위한 수학】 12. 벡터미적분학 - 스토크스 정리 (0) | 2025.12.07 |
| 【물리학을 위한 수학】 10. 벡터미적분학 - 컬(회전) <PART 1> (0) | 2025.12.01 |
| 【물리학을 위한 수학】 09. 벡터미적분학 - 발산 정리 (0) | 2025.11.29 |
| 【물리학을 위한 수학】 08. 벡터미적분학 - 다이버전스(Divergence) <PART 2> (0) | 2025.11.25 |





