Herald-Lab
【물리학을 위한 수학】 12. 벡터미적분학 - 스토크스 정리 본문

벡터장 F가 존재하는 공간에서 임의의 폐곡선 C를 따라 선적분한 총 서큘레이션(circulation) 값은 폐곡선 C의 내부에서 curl을 면적분한 값과 같은 데 이를 스토크스 정리(Stokes' Theorem)라 한다. 이름은 아일랜드 출신의 물리학자 조지 스토크스(Sir George Stokes, 1819-1903)에서 따왔다.

스토크스 정리의 정의와 간단한 증명
Definition and Simple Proof of Stokes' Theorem
스토크스 정리 정의
스토크스 정리는 divergence theorem와 매우 논리적으로 유사한 정리로 우선 발산정리에 대해 다시 한 번 생각해보자.

발산정리에서 Φ_F는 flux로 폐곡면 S를 통과하는 벡터장 F의 면적분(S)으로 정의했다. 여기서 폐곡면에 대한 면적분 기호(∮_S)로 식을 다시 쓰면 아래와 같다.
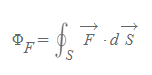
스토크스 정리에서 flux와 대응되는 값으로 서큘레이션(circulation)을 들 수 있다.
서큘레이션이란 폐곡선 C를 따라 적분한 벡터장의 선적분 값으로 공식은 면 S대신 곡선 길이 r로 치환하여 쓴다.

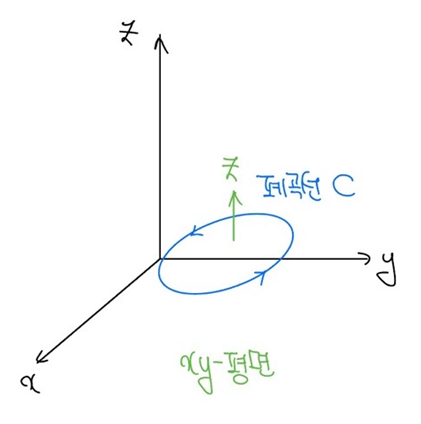
xy-평면에 대한 폐곡선은 [그림 1]과 같이 나타나며, 폐곡선을 따라 발생하는 회전의 방향은 z축으로 나타난다.
또한 스토크스 정리는 폐곡선 C 내부의 면에서 curl을 적분한 값 g가 Γ_F와 같음을 증명한다.
스토크스 정리

■
벡터장 F가 있는 공간에 임의의 폐곡선 C를 그린 다음, C를 따라 벡터장 F의 circulation을 구하기 위해 Stokes' theorem을 사용한다.
- 벡터장 F의 폐곡선 주위에 대해 선적분 한 것은, 벡터장의 curl을 열린 면 S에 걸쳐 면적분 한 것과 같다.
스토크스 정리에 관한 간단한 증명
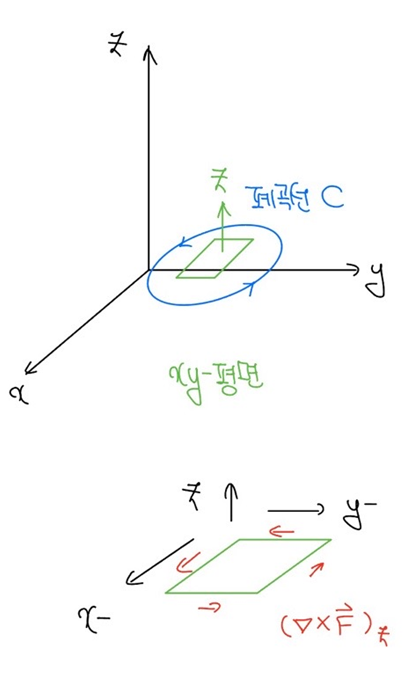
스토크스 정리의 두 가지 식이 서로 항등식임을 증명하기 위해 [그림 2]와 같은 가장 간단한 상황을 가정하자.
- 벡터장 F가 있는 공간에 임의의 폐곡선 C를 그렸을 때 아주 작은 미소면적인 xy-평면을 가정할 수 있고, 이 면적에서의 curl은 +z축을 따라 반시계 방향으로 회전한다.
여기서 curl은 단위벡터 z축만의 것이므로 다음과 같이 식을 간단하게 쓸 수 있다.

- P, Q는 2차원 평면에서 curl 공식을 유도할 때 사용한 기호이다.

xy-평면은 폐곡선 C 내부에 들어갈 수 있는 미소면적으로 폐곡선 C로 묶인 면적 전체를 [그림 3]과 같이 덮을 수 있다. 위의 그림에서는 4개의 연두색 미소면적을 예로 드는데, 여기서 재미있는 사실은 회전의 표현에 있어서 (1), (2)과 (3), (4) 미소면적 간에 모두 같은 방향(반시계 방향)으로 회전하더라도 서로 상쇄되는 구간이 있다는 점이다.
- 폐곡선 C로 묶인 '선' 이외에는 모두 '내부'로 내부의 curl 회전방향은 모두 상쇄된다. ⇒ 따라서 xy-평면의 가장자리 부분인 선에만 curl의 회전 요소가 남게 된다.

curl의 알짜값은 결국 전체 폐곡선 C의 circulation으로 나타나는 데, 이는 xy-평면 요소 전체를 면적분(S)한 것과 같고 식은 아래와 같다.
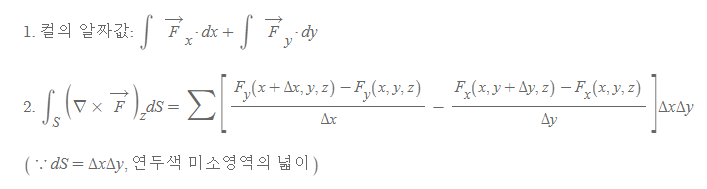
'수학 > 물리학을 위한 수학' 카테고리의 다른 글
| 【물리학을 위한 수학】 14. 적용: 사망시각의 추정 (변수분리형 미분방정식) (0) | 2025.12.27 |
|---|---|
| 【물리학을 위한 수학】 13. 변수분리형 미분방정식 (0) | 2025.12.27 |
| 【물리학을 위한 수학】 11. 벡터미적분학 - 컬(회전) <PART 2> (0) | 2025.12.05 |
| 【물리학을 위한 수학】 10. 벡터미적분학 - 컬(회전) <PART 1> (0) | 2025.12.01 |
| 【물리학을 위한 수학】 09. 벡터미적분학 - 발산 정리 (0) | 2025.11.29 |




