Herald-Lab
【물리학을 위한 수학】 10. 벡터미적분학 - 컬(회전) <PART 1> 본문

벡터미적분학에서 벡터장을 del operator와 함께 곱하는 방법으로 두 가지를 소개하였다: (1)스칼라곱(내적), (2)벡터곱(외적).
첫 번째 연산법으로 델 연산자와 벡터장을 dot product로 구하면 divergence를 얻을 수 있었다. 그리고 지금부터는 두 번째 연산법으로 델 연산자와 벡터장의 cross product를 한 결과 값인 컬(curl)을 다룬다.
- 컬(curl): 회전, 벡터장의 회전 강도 및 방향을 나타내는 벡터 연산으로 단위 면적 당 회전하는 장의 최대값 및 최대값이 나타내는 방향을 가리킨다.
- curl은 델 연산자와 벡터장의 외적으로 계산한다.
컬
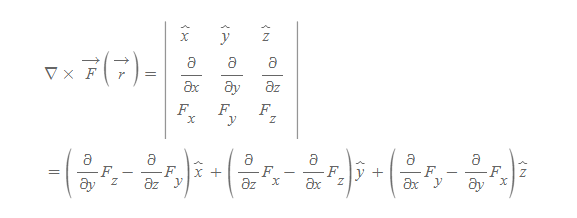
■
curl 식에 등장하는 3x3 행렬식(determinant)은 [그림 1]과 같이 계산한다.
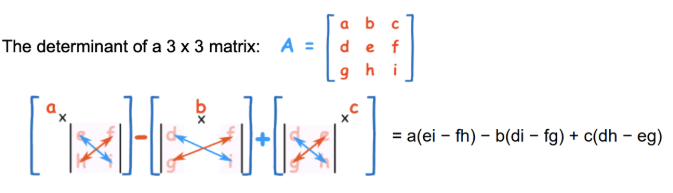
curl 연산은 벡터장에서만 작용하고, 연산의 결과로 또 다른 벡터를 산출한다.
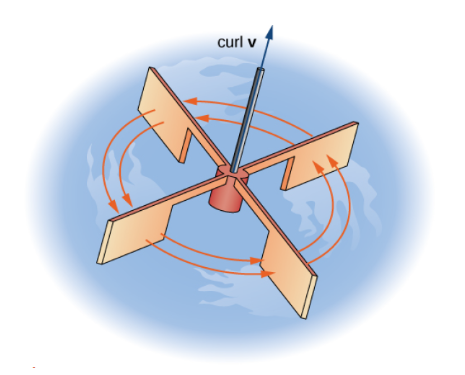
- 물리적으로 curl은 어떠한 장에서의 임의의 미소사각영역을 가정하였을 때, 이것에 수직한 축 주위로 벡터함수가 어떻게 순환하는 지를 알려준다[그림 2].
예를 들어 유체가 흐르는 벡터장의 각 지점은 독특한 속도 벡터를 가질 것이고, 여기에 만약 직선의 나뭇가지를 떨어뜨린다면, 나뭇가지를 둘러싼 유체의 속도벡터 차이 때문에 나뭇가지는 '회전'을 할 것임을 쉽게 알 수 있다.
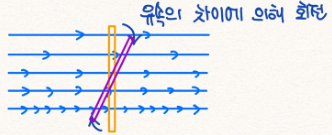
유체장의 흐름 방향에 의해 [그림 3]의 나뭇가지는 오른쪽으로 움직일 것이다. 하지만 유체장에서의 인접한 속도벡터 차이 때문에 나뭇가지는 단순한 병진운동이 아닌 회전하며 이동할 것이며, curl은 이러한 회전이 무슨 방향(시계 방향 또는 반시계 방향)으로 얼마나 빠른 지에 대해 설명해준다.
컬의 해석
평면 영역 위에서, 압축되지 않는 액체유동의 회전 방향은 (1)z-축 성분과 (2)오른손 법칙을 활용하여 그 방향성을 정의할 수 있다.
- 반시계 방향 회전은 양수 부호로 취급한다.
- 시계 방향 회전은 음수 부호로 취급한다.
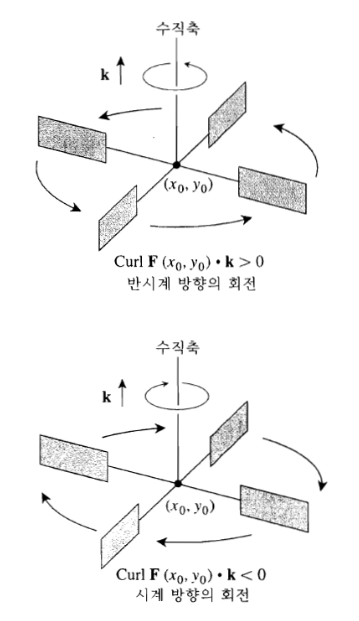
물이 얇은 층으로 xy-평면 상의 한 영역에서 움직일 때, [그림 4]와 같은 풍차를 (x_0, y_0)지점에 설치했다고 하자.
- 풍차의 회전축은 z-축에 따라 놓였다.
- 풍차의 회전축은 xy-평면에 수직하여 (x_0, y_0) 지점에 설치되어 회전시킨다.
- curl은 풍차의 회전축을 중심으로 풍차의 날개가 얼마나 빠르게 어느 방향으로 회전하는 지를 보여준다.
점 (x, y) 지점에서 벡터장 F가 아래와 같을 때,
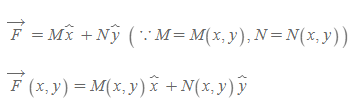
z 성분은 curl을 활용해 아래와 같이 구하며, 이는 벡터장 F의 순환밀도(circulation density)라고도 한다.
평면 벡터장의 순환밀도
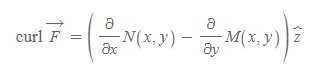
■
위의 순환밀도가 양수이면 반시계방향으로 회전하고, 음수이면 시계방향으로 회전한다.
그리고 그 크기가 클수록 더욱 더 빠르게 회전한다.
'수학 > 물리학을 위한 수학' 카테고리의 다른 글
| 【물리학을 위한 수학】 12. 벡터미적분학 - 스토크스 정리 (0) | 2025.12.07 |
|---|---|
| 【물리학을 위한 수학】 11. 벡터미적분학 - 컬(회전) <PART 2> (0) | 2025.12.05 |
| 【물리학을 위한 수학】 09. 벡터미적분학 - 발산 정리 (0) | 2025.11.29 |
| 【물리학을 위한 수학】 08. 벡터미적분학 - 다이버전스(Divergence) <PART 2> (0) | 2025.11.25 |
| 【물리학을 위한 수학】 07. 벡터미적분학 - 다이버전스(Divergence) <PART 1> (0) | 2025.11.23 |




