Herald-Lab
【물리학을 위한 수학】 14. 적용: 사망시각의 추정 (변수분리형 미분방정식) 본문

법의학(法醫學, forensic science)에서는, 살인 사건 현장에서의 시체 체온과 주변 온도가 어떻게 변하는 지 이해함으로써 사망 또는 살해 시간을 추정할 수 있다. 그리고 이때 쓰이는 가장 기본적인 수학적 모델이 바로 뉴턴의 냉각법칙(Newton's law of cooling)이다.
살인사건에서 검시관에서 주어지는 데이터는 크게 다음과 같다.
- 사체는 생물의 항상성이 깨진 상태로, 체온이 주변 기온과 같은 온도가 될 때까지 열에너지를 계속 방출할 것이다.
- 피살자는 대개 섭씨 25도씨의 방에 있고, 사망 전까지는 정상적인 체온(섭씨 37도씨)을 유지한다고 가정한다.
사망 후 체온하강
Postmortem Body Cooling
뉴턴의 냉각법칙에 앞서 우선 인체의 일반적인 체온 하강에 대해 논의하기 위해 아래 논문을 참고하였다.
출처: Time of Death Estimation from Temperature Readings Only: A Laplace Transform Approach (Marianito R. Rodrigo, 2014)

사망 후 인체의 체온 하강은 [그림 1]과 같이 시그모이드 함수를 그린다. 시그모이드 함수에 따르면 사망 직후의 체온은 비교적 천천히 감소하는데, 이는 크게 두 가지 물리적 요인을 포함한다.
- 사망 후에도 생성하는 장기의 잔여 열생산
- 신체의 열전도율과 열용량
특히 신체의 열전도에 있어서 냉각은 (1)신체에서 표면적이 비교적 작은 피부 표면에서의 대류(convection) 때문이며, 사망 직후 체온이 천천히 감소하는 것은 (2)피부보다 표면적이 넓은 여러 신체층(body layers)이 신체 중심부의 열을 안정적으로 전도(conduction)하기 때문이다.
- 체온은 [그림 2]와 같이 구획(compartment)화가 가능하고, 열에너지의 흐름은 온도가 높은 영역에서 낮은 영역으로 일방향성을 갖는다.
- 신체의 온도 항상성은 구획 내의 체온 보존되는 형태로 열에너지가 지속적으로 흐르는 상태를 뜻한다.

뉴턴의 냉각법칙
Newton's Law of Cooling
뉴턴의 냉각법칙이란, 어떤 물체의 온도는 주변 온도의 차이에 비례하는 속도로 열에너지를 방출한다는 것이고 수식으로 다음과 같이 나타낸다.
뉴턴의 냉각법칙

■
<물리량>
- T(t): 시간 t가 지난 후의 시체의 온도
- T_s: 주변환경(surroundings)의 온도 ⇒ 대개는 일정하다고 가정한다.
- k: 냉각비율 상수
즉, 온도의 변화율이란 주변 온도와의 차이에 비례하게 발생한다는 것으로 cooling law는 변수분리형 미분방정식에 해당한다.
변수분리형 미분방정식의 풀이법에 따라 우선 T 해(solution)를 구해보자.
[1] 변수 분리

[2] 양변 적분
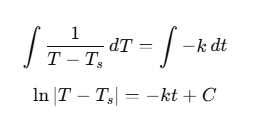
[3-1] 계산: 지수함수 적용

[3-2] 계산: 부정적분 상수 C 구하기 (초기조건 활용)
여기서 t는 시간(단위: 분)으로 만약 t=0일 때를 계산하면 다음과 같이 식을 고쳐쓸 수 있을 것이다.

부정적분을 통해 나온 적분 상수는 T(t=0)-T_s (사망 직전의 체온에서 주변환경의 온도를 뺀 값)와 같다.
[4] 결과: 해
T(t=0)을 T_0라 둘 때, 적분 상수를 포함한 해 T는 다음과 같이 구할 수 있다.
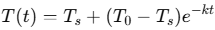
사망추정시간(사망 후 경과시간)
미분방정식의 해인 T(t)는 경과시간 t후에 사망자의 온도에 해당한다. 시간 t 후의 측정 온도를 T_m이라고 하였을 때, 식은 우선 아래와 같이 고칠 수 있다.

여기서 t[단위: 분]가 바로 사망 후 경과시간으로 이것을 풀기 위해서 e^-kt항을 따로 빼낸다.

다음 양변에 자연로그를 취한다.
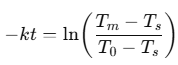
마지막으로 여기서 t를 구하기 위해 다시 양변에 -(1/k)를 곱해주면, 사망 후 경과시간을 구하는 일반식이 나온다.
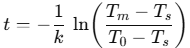
사망 후 경과시간

■
- k: 경험적 냉각상수
- T_m: 사망 후 시간 t만큼 지났을 때의 시체의 온도
- T_s: 주변 온도
- T_0: 사망 직전 체온(일반적으로 사람은 섭씨 37도로 측정된다.
경험적 냉각상수 구하기
만약 25도씨의 방안에 35도씨의 사체를 처음 발견하였고, 이후 80분 뒤에 32도씨로 떨어진 경우, 경험적 냉각상수 k를 다음과 같이 구할 수 있다. (단, 인간의 사망 전 정상체온은 섭씨 37도로 가정한다.)
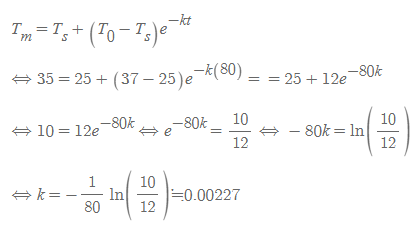
이를 사망 후 경과시간에 넣으면 사체를 처음 발견한 시간으로부터 사망 후 경과시간을 추정할 수 있다.
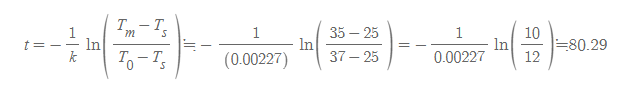
시간은 분 단위였기 때문에, 즉 사망 후 경과시간을 약 80.3분이라 계산할 수 있다.
'수학 > 물리학을 위한 수학' 카테고리의 다른 글
| 【물리학을 위한 수학】 16. 적용: 탄소연대측정 (변수분리형 미분방정식) (0) | 2026.01.02 |
|---|---|
| 【물리학을 위한 수학】 15. 적용: RC회로 (변수분리형 미분방정식) (0) | 2025.12.28 |
| 【물리학을 위한 수학】 13. 변수분리형 미분방정식 (0) | 2025.12.27 |
| 【물리학을 위한 수학】 12. 벡터미적분학 - 스토크스 정리 (0) | 2025.12.07 |
| 【물리학을 위한 수학】 11. 벡터미적분학 - 컬(회전) <PART 2> (0) | 2025.12.05 |




