【물리학을 위한 수학】 15. 적용: RC회로 (변수분리형 미분방정식)

사전지식

1. 전자기학 중 회로(circuit) 이론
2. 키르히호프의 법칙
3. RC 회로: 저항기(R)와 축전기(커패시터, 컨덴서, C)가 직렬로 연결된 회로
4. 변수분리형 미분방정식의 풀이

​

​

RC회로: 충전과 방전

RC Circuit: Charging and Discharging

 

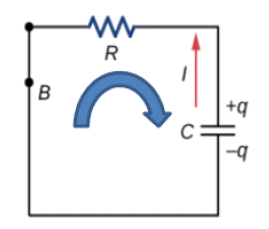
RC회로란, 회로 상 저항기(resistor)와 축전기(capacitor, condenser)가 직렬로 연결된 회로로 [그림 1]과 같은 구조를 갖는다.

 

그림 1. RC회로의 구조와 충전(charge), 방전(discharge) [출처: Openstax University Physics Vol 2 (Ling et al, 1st ed., 2017, p.469)]

 

축전기 충전

그림 2. 축전기 충전

 

 

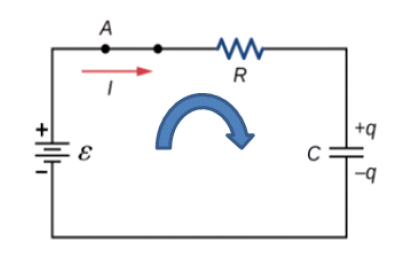
RC회로에서 축전기의 충전단계[그림 2]를 분석해보자.

• 스위치 A가 닫혔을 때, 전류 I가 흐르게 되는데, 이때 임의의 시계방향 이동 화살표(파란색)를 회로에 먼저 그린다. ⇒ 회로 소자를 분석하는 데 기준이 되는 화살표로 전류의 방향과 상관없이 임의로 그려도 된다.
• 전류 I는 전지에서의 기전력 ε에 의해 시계방향으로 이동한다.

​

저항 R과 축전기 C는 전지로부터 나오는 기전력을 소비하고 충전하는 형태로 이용(-)하기 떄문에, 키르히호프의 법칙을 적용하여 아래와 같이 식을 쓸 수 있다.

<물리량>

• ε: 전지 기전력
• q/C: 축전기의 전위차, 축전기의 전기용량 C로부터 유도된 값으로 q는 축전기에 저장된 전하량을 뜻한다.
• IR: 옴의 법칙으로 유도된 저항기에 걸린 전압, I는 회로를 통해 통과하는 전류, R은 저항기의 고유 저항을 뜻한다.

​

전류의 방향과 임의의 화살표가 서로 같은 방향으로 움직일 때, 축전기는 '충전'되고, 저항은 퍼텐셜에너지를 '소비'하여 전압강하를 일으킨다.

• 저항기가 전구인 경우, 퍼텐셜에너지 소비는 전구에 불이 켜지는 식으로 나타날 것이다.

​

여기서 q와 I는 시간에 의존하는 물리량이다.

​

[1] 스위치를 누르는 순간인 t=0일 때, 축전기에 저장된 전하량 q는 0이다.

위의 식을 전류 I에 대해 고쳐쓰면, RC회로의 최고전류 값을 구할 수 있다.

<물리량>

• I_i: RC회로의 최고 전류

​

[2] 축전기의 최대 충전량

한편 축전기가 최대로 충전되면 RC회로에는 더 이상 전류가 흐르지 않는데, 같은 식에서 I를 0으로 취하고, 축전기의 최대 전하량을 Q라 했을 때, 식을 다음과 같이 쓸 수 있다.

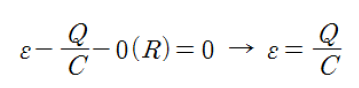
전지 기전력이 축전기에 최대 전위차를 생성한 것이고 이를 RC회로의 최대 전하충전량 Q로 정리하면 아래와 같다.

​

RC회로 최고 전류

■

RC회로 축전기 최대(전하)충전량

■

​

[3] 축전기의 충전단계

전류가 흐르는 중, 축전기가 충전되는 단계를 분석하기 위해 우선 키르히호프 수식에 (1/R)을 곱한다.

 

여기서 전류 I는 dq/dt의 미분식(시간 당 흐르는 전하량)으로도 쓸 수 있다.

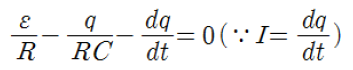
위의 식에서 dq/dt를 좌변항에 두고 양변에 (-1)을 곱하면,

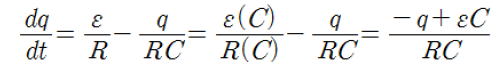
로 식이 정리되고, 미분방정식 꼴은 아래와 같다.

위의 식은 변수 분리가 가능한 형태로 변수 분리한 뒤 적분해보자.

 

 

​

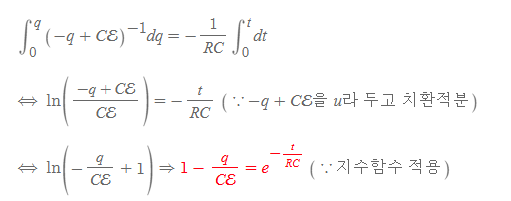
위 빨간식의 좌변항을 풀기 위해 1을 Cε/Cε로 고쳐쓰고,

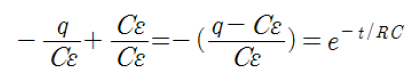
다음 양변에 -Cε를 곱하면, 충전 시 시간에 따른 전하량 함수를 구할 수 있다.

충전 시, 시간에 따른 축전기의 충전 전하량 함수

■

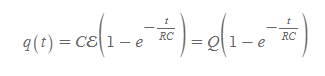
위 식의 Cε는 RC회로 축전기 최대전하충전량임을 이미 알고 있다.

​

​

축전기 방전

그림 3. 축전기 방전

 

 

RC회로에서 전지가 사라지면, 축전기에서는 방전이 발생한다.

• 회로에 전지가 없어진 것을 제외하고는 이전과 거의 같은 상황이다. ⇒ 전지 기전력 항을 지운다.

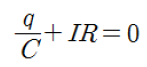
축전기가 충전된 상황에서 시계방향 이동 화살표는 여전히 작동[그림 3]하며, 충전된 축전기가 이제 전지의 역할을 하므로 양전하 +q가 충전된 판으로부터 전류 I가 보내진다.

• 축전기에서 발생한 전류는 시계방향 이동 화살표와 반대 방향이다.

​

저항기 항의 전류 I을 dq/dt로 변환한 뒤, 위 식을 아래와 같이 변형한다.

​​

다음 빨간 식의 양변에 (1/R)을 곱하고, 미분방정식 꼴로 변경하면,

위와 같이 정리된다.

​

다음 미분방정식에 대해 변수분리를 한 뒤 적분을 할건데, 이때 초기조건은 t=0이고, q=Q(축전기가 최대로 충전된 상태)이다.

​​

따라서, 방전 시 시간에 따른 축전기의 방전 전하량 함수는 다음과 같다.

​

방전 시, 시간에 따른 축전기의 방전 전하량 함수

■

​

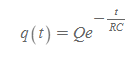
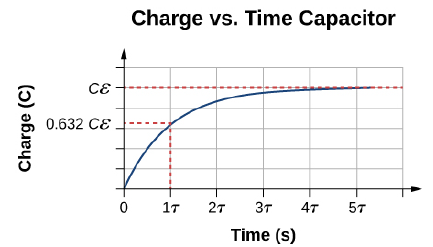
시간에 따른 축전기의 충전 전하량 함수와 방전 전하량의 함수는 각각 [그림 4]와 [그림 5]와 같이 그려진다.

​

그림 4. 시간에 따른 축전기의 충전 전하량 함수  [출처: Openstax University Physics Vol 2 (Ling et al, 1st ed., 2017, p.471)]

 

 

그림 5. 시간에 따른 축전기의 방전 전하량 함수 [출처: Openstax University Physics Vol 2 (Ling et al, 1st ed., 2017, p.472)]