Herald-Lab
【물리학을 위한 수학】 16. 적용: 탄소연대측정 (변수분리형 미분방정식) 본문

탄소-14
Radiocarbon

방사성의 원자는 시간이 지나며 안정된 원자로 자발적으로 붕괴한다. 과정은 무작위적이지만, 매우 큰 집단 전체에서의 평균적 감소율은 일정한 규칙을 따르는 것을 활용한다.
- 지구의 성층권은 항상 고에너지의 우주광선(cosmic radiation)으로 노출되어 있는데, 이 우주광선은 중성자(neutron)을 방출시킬 정도로 매우 강하고 대기로부터 방출된 중성자가 공기 중의 질소와 충돌하여, 그 일부가 방사능 물질인 탄소-14로 바뀐다. ⇒ 중성자에 의한 질소의 양성자 잃음 및 중성자 포획(neutron capture)
- 방사성 탄소 연대측정(radiocarbon dating)*: 탄소화합물 중 탄소의 극히 일부에 포함된 방사성 동위원소인 탄소-14의 조성비를 측정하여 만들어진 연대를 추정한다.
- 탄소-14의 반감기는 약 5730년이며, 이를 이용하면 약 6만년 전까지의 연대를 거꾸로 유추할 수 있다.
- 탄소-14의 양이 인위적으로 변한 시점은, 1950년으로 전세계적으로 퍼진 핵실험에 기인한다.

|
방사성 탄소 연대측정
1940년대 후반 시카고 대학교의 교수인 미국인 물리화학자 윌러드 리비(Willard Libby, 1907-1980)에 의해 발명(1949)되었다. 이 기술은 불안정한 방사성 탄소-14가 [그림 1]과 같이, 지구 대기 중에서 우주선(cosmic ray)이 대기의 질소와 상호작용할 때마다 지속적으로 생성된다는 사실에 기반한다. 생성된 탄소-14는 대기의 산소와 결합하여 방사성 이산화탄소를 형성하고, 광합성을 통해 식물에 흡수된다. 물론 이를 먹은 동물 또한 탄소-14가 몸에 축적된다.
이처럼 동식물의 섭취에 의해 탄소-14는 최종적으로 유기물에 잔류하게 되는데, 그 시점부터 그 안에 포함된 탄소-14의 양은 방사성 붕괴에 의해 점차 감소하기 시작한다. 나무 조각 또는 뼈와 같이 죽은 동식물에서 채취한 시료에 포함된 탄소-14의 양을 측정하면 생물체의 사후 시점을 계산할 수 있다.
|
탄소연대측정
Radiocarbon Dating
탄소연대측정에서 방사성을 띤 원자가 붕괴 시 방사형태의 에너지로 전환되며, 질량의 변화속도는 질량 자체의 값에 비례한다.

<물리량>
- N': 시간당 질량변화량(질량 변화속도)
- k: 방사능 물질 종류에 따른 상수
위의 식은 변수분리형 미분방정식의 기본형으로 다음과 같이 변형 가능하다.
양변 적분
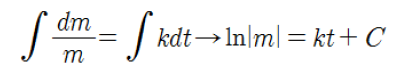
여기서 질량 m은 항상 양의 값을 가질 것이다. 따라서 적분 식을 다음과 같이 풀 수 있다.
계산: 적분결과와 지수함수
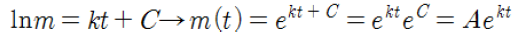
여기서 A는 e^C와 같다.
이제 주어진 방사능 물질에 관한 k 값과 A를 결정하기 위해 두 개의 측정값을 사용하도록 한다.
- 시간 t=0일 때 방사능 물질의 초기 질량을 M으로 둔다.
- 시간 t=T가 지났을 때, 방사능 물질의 나중 질량은 M_T라 한다.
두 개의 미지수를 구하기 위한 두 개의 측정값을 사용하면, 각각 아래와 같이 계산된다.
계산: 초기조건과 나중조건 활용
먼저 첫 번째 초기 조건을 쓰면 A를 계산할 수 있다.
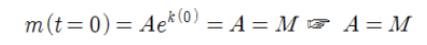
다음 두 번째 나중 조건을 쓰면 k값이 나온다.
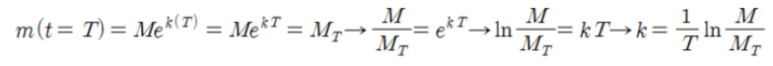
계산: 미지수 보충
적분결과 값에 위의 두 값을 대입하자.
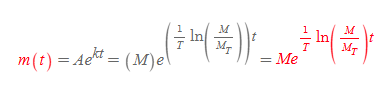
반감기
radiocarbon dating의 또 다른 개념으로 우리는 반감기의 특징을 활용해야 한다. 반감기(half-life)란, 질량이 에너지로 방출되어 정확하게 절반이 남게될 때 시간을 의미한다. T_half라고 적는다.

반감기의 위와 같은 특징을 활용해 t 시간에서의 방사능 물질의 질량 값 m(t)를 다음과 같이 고쳐쓸 수 있다.
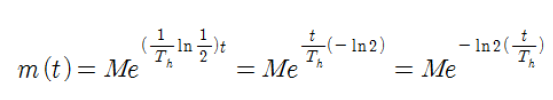
탄소-14의 반감기는 앞서 5730년이라고 했다.
t시간에서의 탄소-14 질량값
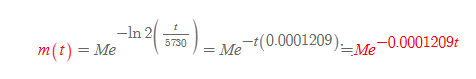
■
위의 식을 이용하면, 이제 고대 유물 또는 화석의 생성연대를 추정할 수 있다.
만약 어떤 유물의 탄소-14 비율이 30%인 것을 식으로 쓰면 아래와 같이 쓸 수 있다.
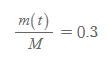
이를 t시간에서의 탄소-14 질량값에 대입하고 '걸린 시간' t를 구하면 다음과 같다.

여기서 t란 1g의 방사능탄소가 붕괴되어 현재의 양까지 도달하는 데 걸린 시간으로 보통 k에 의해 '년(年, year)'이고, 따라서 이 유물은 약 9960년 전에 만들어졌다고 계산할 수 있다.
'수학 > 물리학을 위한 수학' 카테고리의 다른 글
| 【물리학을 위한 수학】 17. 1계 선형 미분방정식 (0) | 2026.01.03 |
|---|---|
| 【물리학을 위한 수학】 15. 적용: RC회로 (변수분리형 미분방정식) (0) | 2025.12.28 |
| 【물리학을 위한 수학】 14. 적용: 사망시각의 추정 (변수분리형 미분방정식) (0) | 2025.12.27 |
| 【물리학을 위한 수학】 13. 변수분리형 미분방정식 (0) | 2025.12.27 |
| 【물리학을 위한 수학】 12. 벡터미적분학 - 스토크스 정리 (0) | 2025.12.07 |




