Herald-Lab
【물리학을 위한 수학】 17. 1계 선형 미분방정식 본문

1계 선형 미분방정식의 형태
Form of 1st Order Linear Differential Equation
1계 선형 미분방정식(first order linear DE): 종속변수가 한 번 미분이 되고, 종속변수와 그 도함수의 계수가 독립변수에만 의존하는 미분방정식
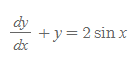
만약 위와 같은 식이 있을 때, 이는 1계 선형미분방정식의 형태를 만족한 것인데, 1계 선형미분방정식의 형태는 다음과 같다.

- y=y(x)는 미지의 함수이다.
- P(x)와 Q(x)는 연속 함수이다.
- 미분계수 y'와 y는 선형적으로 포함된 형태이다.
위의 식에서 Q(x)=0이라면 동차방정식, Q(x)≠0이라면 비동차방정식이라 한다.
- 또는 Q(x)=0인 식을 제차(homogeneous), Q(x)≠0인 식을 비제차(non-homogeneous) 1계 선형미분방정식이라도 부른다.
동차 1계 선형미분방정식
y'+P(x)y=Q(x)에서 Q(x)=0이라면 이는 동차 1계 선형미분방정식이라 한다.
동차 1계 선형미분방정식의 형태

■
동차 1계 선형미분방정식의 일반해는 아래와 같은 과정을 통해 풀이한다.
[1] P(x)y를 우변으로 넘기기

[2] 변수분리형 방정식으로 고치기
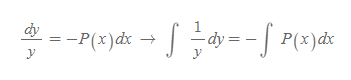
[3] 일반해 y 구하기
변수분리형 방정식에서 일반해를 구한 것과 마찬가지로 위의 식을 최종적으로 y에 대해 풀면 다음과 같이 계산된다.
- 양변 적분

- 양변 지수함수
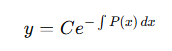
동차 1계 선형미분방정식의 해

■
<물리량>
- C: 임의상수
예를 들어, y'+3y=0이라는 동차 1계 선형미분방정식이 있다고 하자. 여기서 P(x)는 3이고, 따라서 일반해는 아래와 같이 매우 쉽게 구해진다.

한편 y'+2xy=0과 같은 동차 1계 선형미분방정식이 주어졌을 때, P(x)=2x이고,
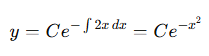
로 일반해 계산이 가능하다.
비동차 1계 선형미분방정식
한편 Q(x)가 0이 아닌 경우, 이는 비동차 미분방정식이라 하며, y'+P(x)y=Q(x)는 특별히 비동차 1계 선형미분방정식이라 한다.
비동차 1계 선형미분방정식의 형태

■
위와 같은 식의 일반해는 아래와 같이 푼다.
[1] 적분인자(integrating factor)
비동차 1계 선형미분방정식의 형태의 모든 항에 적분인자라는 특수한 값을 곱한다.
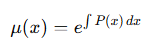
위의 적분인자를 형태의 모든 항에 곱하면,

과 같이 계산된다.
- 좌변을 미분하기 위하여 곱함수미분법을 활용했다.
[2] y(x)에 대해 풀이
적분인자를 모든 항에 대해 곱해줌으로써 아래와 같은 식을 유도할 수 있다.
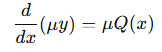
이제 이 식의 양변을 다음과 같이 적분한다.
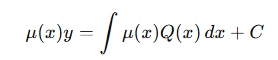
마지막으로 식을 y(x)에 대해 풀어주면, 비동차 1계 선형미분방정식의 해를 구할 수 있다.

비동차 1계 선형미분방정식의 해
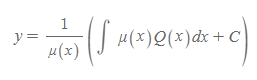
■
만약 y'+y=x와 같은 비동차 1계 선형미분방정식을 예로 들면, 풀이 후 최종 해는 다음과 같이 계산된다.
[1] 적분인자
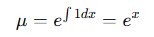
위와 같이 구해진 적분인자를 주어진 식의 양변에 곱해준다.
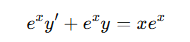
식의 좌변은 곱의 미분과 같이 떄문에, 식을 다음과 같이 변형할 수 있다.
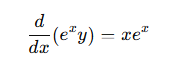
[2] y(x)에 대해 풀이
좌변을 곱의 미분 식으로 변경했기 때문에, 식의 양변을 다음과 같이 적분한다.
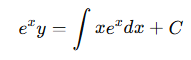
비동차 1계 선형미분방정식의 해를 구해줘야 하기 때문에, 최종 값은 다음과 같다.

'수학 > 물리학을 위한 수학' 카테고리의 다른 글
| 【물리학을 위한 수학】 16. 적용: 탄소연대측정 (변수분리형 미분방정식) (0) | 2026.01.02 |
|---|---|
| 【물리학을 위한 수학】 15. 적용: RC회로 (변수분리형 미분방정식) (0) | 2025.12.28 |
| 【물리학을 위한 수학】 14. 적용: 사망시각의 추정 (변수분리형 미분방정식) (0) | 2025.12.27 |
| 【물리학을 위한 수학】 13. 변수분리형 미분방정식 (0) | 2025.12.27 |
| 【물리학을 위한 수학】 12. 벡터미적분학 - 스토크스 정리 (0) | 2025.12.07 |




