Herald-Lab
【물리학을 위한 수학】 13. 변수분리형 미분방정식 본문

미분방정식 소개
Introduction to Differential Equation
미분방정식(differential equation, DE): 미지의 함수와 그 도함수로 구성된 식
- 미지의 함수 y=f(x)와 도함수 dy/dx 또는 d^n(y)/dx^n 간의 관계성을 드러낸 모든 형태의 식을 미분방정식이라 한다.
- 수학적 모델(mathematical model)*을 활용하는 모든 분야에서 발견되는 식으로, 과학, 공학, 인문학 등에 널리 활용된다.
|
수학적 모델
수학적 모델이란 구체적인 체계(concrete system)를 수학적 개념과 언어를 사용하여 추상적(abstract)으로 기술한 것으로, 수학적 모델은 통계, 게임 이론 모형, 미분방정식 등 여러 가지 형태를 취할 수 있다. 물리학을 비롯한 자연과학에서 수학적 모델은 아래와 같은 요소(following elements)를 포함한다.
수학적 모델을 개발하는 과정은 수학적 모델링(mathematical modeling)이라 한다. |
미분방정식의 목표
미분방정식은 미분 형태의 변화율(dy/dx)로 주어진 관계에서, 미지의 함수 y를 '복원'하여 복잡한 자연계 현상의 시공간적 거동을 예측하는 데 목표를 둔다.
예를 들어,
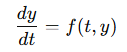
와 같이 시간을 독립변수로 하는 변화율로만 주어진 식을

꼴로 만들어, y를 시간에 대한 명시적 함수로 다양한 값들을 정량화 할 수 있다.
미분방정식의 분류
미분방정식은 독립변수의 개수에 따라 크게 두 가지로 나뉜다.
- 상미분방정식(ordinary DE, ODE): 1변수 함수 ⇒ 구하려는 함수가 1개의 독립변수만 가지는 방정식
- 편미분방정식(partial DE, PDE): n변수 함수, 다변수 함수 ⇒ 여러 개의 독립 변수로 구성된 함수와 그 함수의 편미분으로 연관된 방정식
고전역학에서 뉴턴의 운동 제2법칙 공식은 상미분방정식 형태로 나타낼 수 있다.
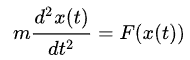
- 질량 m의 물체 운동에 관하여, 시간 t에 대해 거리가 x(t)이고 힘의 크기는 F이다.
- 여기서 독립변수는 t만 존재하므로 1변수 함수에 대한 상미분방정식이다.
미분방정식에 포함된 도함수 중 미분 횟수가 가장 많은 것이 n번일 때, 이 식을 n계 미분방정식이라 한다.
- n은 계수(order)라 한다.
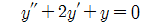
위의 식은 2계 미분방정식이며, 뉴턴의 운동 제2법칙 식 또한 2계이다.
제차 미분방정식과 비제차 미분방정식
미분방정식은 방정식의 형태에 있어, 외부항의 존재 여부에 따라 (1)제차(homogeneous)와 (2)비제차(non-honmogeneous)로 또한 구분할 수 있다.
1. 제차 미분방정식(제차 방정식)
- 미분방정식에서 식의 오른쪽이 0이 되는 형태로 미분항과 미지함수만 존재한다.
- 외부항이 존재하지 않는다.
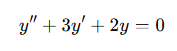
제차방정식의 표현은 바깥에서 추가적으로 작용하는 에너지나 자극이 없이 시스템의 내부성질로만 움직이는 특성을 반영한다.
- 물리학에서 system의 내부성질이란, 관성, 탄성, 전하 분포 등을 뜻한다.
- 시스템 내부에 존재하는 형태, 배열, 에너지에 따라 스스로 변화를 일으키는데, 제차방정식은 이를 반영한다.
2계 제차 미분방정식의 대표로 감쇠가 없는 스프링 진동자(undamped oscillator)를 들 수 있다.
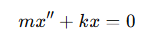
- 의미: 질량 m인 물체가 스프링 상수 k인 물체에 연결된 경우를 표현한 미분방정식
2. 비제차 미분방정식(비제차 방정식)
- 미분방정식에서 식의 오른쪽이 0이 아닌 형태
- 외부항이 존재한다.
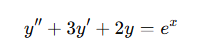
비제차방정식의 표현은 외부에서의 추가적인 에너지나 자극(강제항)을 포함하여 시스템의 내부성질과 외부입력이 모두 반영된 특성을 반영한다.
- 물리학에서 강제항(forcing term)이 되는 것들로 일정하게 주어지는 힘, 일정 전압 등이 있다.
따라서 비제차 미분방정식의 일반해(solution)은 시스템의 내부성질과 외부입력을 모두 반영한 제차해 + 특수해의 형태로 구성된다.

- 제차해: 미지함수와 그 미분항으로 이루어진 선형 연산자 = 0 (제차방정식)의 해
- 특수해: 외부항인 f(x)를 만족하는 해
2계 비제차 미분방정식의 대표로 외력 F를 받는 스프링 진동자를 들 수 있다.
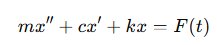
고전역학에서 뉴턴의 운동 제2법칙은 결국 '비제차 2계 상미분방정식'에 속한다.
변수분리형 미분방정식
Separable Differential Equation (Separable DE)
변수분리형 미분방정식은 미지함수 y와 독립변수 x를 서로 다른 곱 형태로 분리 가능한 식이다. 미지의 함수 y를 복원하기 위해 다음의 식
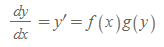
을 아래와 같이 분리가 가능해보자. 이처럼 양변을 분리할 수 있으면 변수분리형이라 한다.
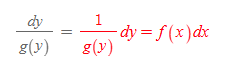
위의 변수분리형 미분방정식은 1계 상미분방정식이다.
변수분리형 미분방정식 풀이
변수분리형 미분방정식은 크게 4단계를 거친다.
예를 들어 dy/dx=xy라는 식이 있다고 하자.
[1] 변수 분리
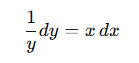
[2] 양변 적분
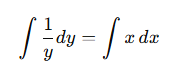
변수분리형 미분방정식에서 양변 적분은 대부분 가장 간단한 형태의 부정적분표를 따른다.

과정 [2]에서 적분은 부정적분표에서 4번(x항)과 5번(y항)을 따른다.
[3-1] 계산: 적분 결과와 지수함수
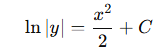
양변에 적분을 하면 자연로그(자연로그 밑 e를 포함한 로그)를 포함한 식이 나오는 데, y를 구하기 위해서 양변에 지수함수를 취한다.
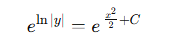
우변 항은 아래와 같이 정리할 수 있다. (지수법칙 e^(a+b)=e^a × e^b 활용)
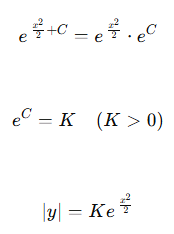
e^C는 양수 상수이므로 이를 새롭게 정의한 K 역시 양수 값으로 한정할 수 있다.
[3-2] 계산: 절대값 지우기
식 |y|의 절대값을 풀기 위해 다시 아래와 같이 식을 고쳐쓴다.
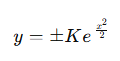
여기서 +-K는 하나의 임의 상수 C로 다시 묶을 수 있는데, K>0이면서, +-K 값은 0을 제외한 모든 실수값을 덮을 수 있기 때문에 새로운 상수 C를 적용하면 최종적으로 다음과 같이 미지함수 y를 정리할 수 있다.
[4] 결과: 미지함수 y
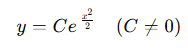
'수학 > 물리학을 위한 수학' 카테고리의 다른 글
| 【물리학을 위한 수학】 15. 적용: RC회로 (변수분리형 미분방정식) (0) | 2025.12.28 |
|---|---|
| 【물리학을 위한 수학】 14. 적용: 사망시각의 추정 (변수분리형 미분방정식) (0) | 2025.12.27 |
| 【물리학을 위한 수학】 12. 벡터미적분학 - 스토크스 정리 (0) | 2025.12.07 |
| 【물리학을 위한 수학】 11. 벡터미적분학 - 컬(회전) <PART 2> (0) | 2025.12.05 |
| 【물리학을 위한 수학】 10. 벡터미적분학 - 컬(회전) <PART 1> (0) | 2025.12.01 |





