Herald-Lab
【물리학을 위한 수학】 05. 벡터미적분학 - 델(나블라) 연산자 본문

벡터미적분학(vector calculus): 벡터 함수와 다변수 함수의 모델링을 다루는 미분적분학의 세부 분야
- 벡터미적분학에서는 새로운 연산자들이 등장하는데, 대표적인 것이 델(del) 연산자이다.
- del operator: 나블라(nabla operator), 미분에서의 d와 마찬가지로 벡터 함수에서 다차원 미분을 위한 연산자, 아일랜드의 수학자 윌리엄 해밀턴(Sir William R. Hamilton, 1805-1865)이 고안했다.
3차원 공간(직교좌표계)에서 델 연산자는 다음과 같이 정의된다.
델 연산자
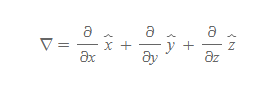
■
del operator에서 ∂는 편미분(partial derivative) 기호로 다변수 함수의 특정 변수를 제외한 나머지를 상수로 취급하여 미분함을 의미한다.
만약 독립변수가 두 개인 경우 u=f(x, y)라 했을 때, 편미분 du는 다음과 같이 계산한다.
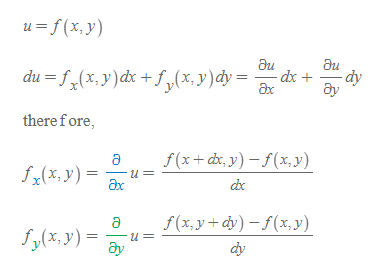
좌표계에 따른 델 연산자 표기
Experssions of the Del Operator in different coordinate systems
델 연산자는 독립변수가 둘 이상일 때 편미분 기호를 활용한 미분연산자로 직교 좌표계에서는 위의 정의와 같이 쓰였다.
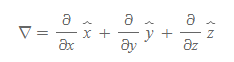
만약 u=f(x, y, z)인 함수에서 미분 du는 다음과 같이 구할 수 있다.
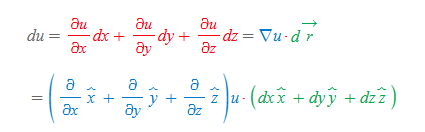
du는 ∇u에 벡터 r을 점곱(scalar dot)을 한 결과와 같다.
- 위의 파란색 식에서 u를 빼면 ∇의 정의를 유도할 수 있다.
- du = ∇u(dot)d(r)은 각 좌표계의 del operator를 구하기 위해 통용되는 일반식이다.
du 일반식
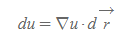
■
- du 일반식은 좌표계와 상관없는 일반적인 정의로 각 좌표계에서의 델 연산자 정의 계산에 된다.
원통좌표계의 델 연산자
원통좌표계의 u=f(ρ, φ, z)라 하였을 때, du는 다음과 같이 계산한다.
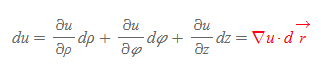
원통좌표계의 del operator를 구하기 위해 du 일반식을 활용한다.
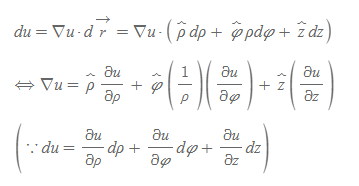
따라서 원통좌표계의 델 연산자 정의는 아래와 같다.
델 연산자(원통좌표계)
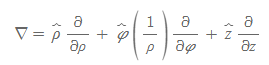
■
구좌표계의 델 연산자
구좌표계의 u=f(r, θ, φ)라 하였을 때, du는 다음과 같이 계산한다.
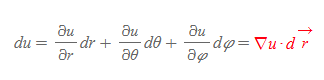
구좌표계의 del operator를 구하기 위해 du 일반식을 활용한다.
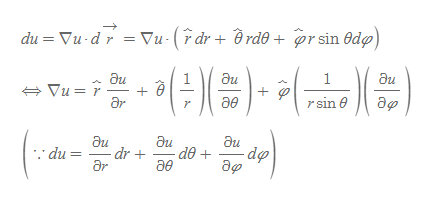
따라서 구좌표계의 델 연산자 정의는 아래와 같다.
델 연산자(구좌표계)
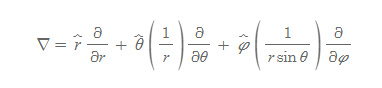
■
앞으로 이 델 연산자를 활용하여 물리학에서 등장하는 장(場, field)을 미분함으로써 다양한 물리학적 의미를 다루도록 한다.
'수학 > 물리학을 위한 수학' 카테고리의 다른 글
| 【물리학을 위한 수학】 07. 벡터미적분학 - 다이버전스(Divergence) <PART 1> (0) | 2025.11.23 |
|---|---|
| 【물리학을 위한 수학】 06. 벡터미적분학 - 그래디언트(Gradient) (0) | 2025.11.22 |
| 【물리학을 위한 수학】 04. 좌표변환 - 3차원 좌표계 (0) | 2025.11.19 |
| 【물리학을 위한 수학】 03. 원운동 해석 (0) | 2025.11.18 |
| 【물리학을 위한 수학】 02. 좌표변환 - 2차원 좌표계 (0) | 2025.11.17 |





