Herald-Lab
【물리학을 위한 수학】 02. 좌표변환 - 2차원 좌표계 본문

단위벡터
Unit Vectors
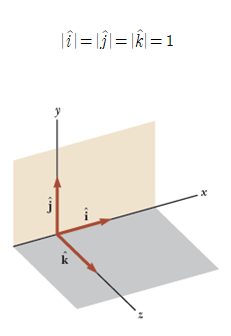
단위벡터(unit vector): 벡터 a의 단위벡터란, 벡터 a와 방향은 같고 크기가 1인 벡터[그림 1]
- x, y, z축에 대해 각각 단위벡터 x, y, z 또는 단위벡터 i, j, k로 표기한다.
- 단위벡터의 크기는 그 종류와 상관없이 항상 1로 둔다.
- 단위벡터의 꺽쇠 모자를 햇(hat)이라 한다.
벡터 a의 단위벡터와 벡터와의 관계는 다음과 같다.
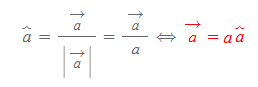
2차원의 좌표계에서 단위벡터는 다음과 같다.
직각좌표계
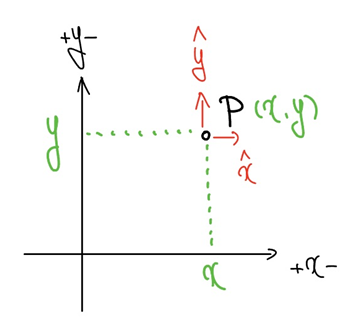
데카르트 좌표계에서 지점 P에서의 단위벡터[그림 2]는 다음과 같다.
- hat x: y는 일정하게 유지한 채 x만 증가하는 방향을 갖는 x 단위벡터
- hat y: x는 일정하게 유지한 채 y만 증가하는 방향을 갖는 y 단위벡터
극좌표계
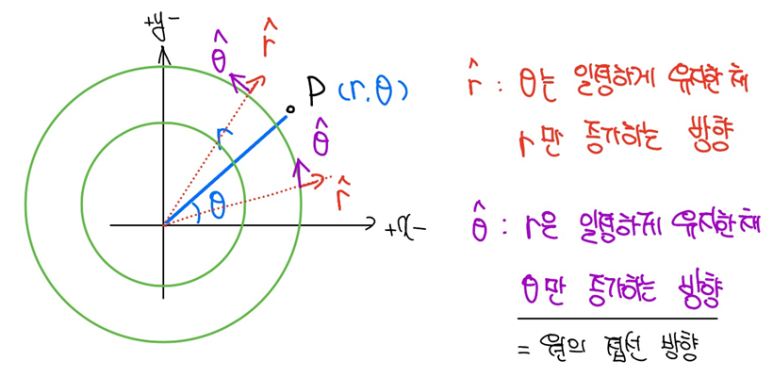
극좌표계에서 지점 P에서의 단위벡터[그림 3]는 다음과 같다.
- hat r: θ는 일정하게 유지한 채 r만 증가하는 방향을 갖는 단위벡터
- hat θ: r은 일정하게 유지한 채 θ만 증가하는 방향(원의 접선방향)을 갖는 단위벡터
내적(점곱)
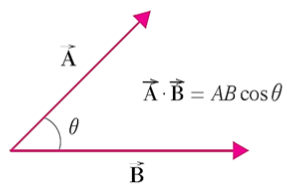
내적(dot product): 점곱, 스칼라곱, 두 벡터를 곱하는 한 가지 방법으로 [그림 4]와 같이 두 벡터를 곱해준다.
- 내적의 결과는 스칼라량으로 스칼라곱으로도 불린다.
- 두 벡터의 각도가 평행일 때 cos0=1이므로 최댓값이 계산된다.
- 두 벡터의 각도가 수직이면 cos90=0이므로 0으로 계산된다.
직각좌표계와 극좌표계에서의 단위벡터 내적은 다음과 같다.

직교좌표계의 특징
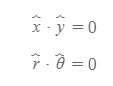
■
2차원 좌표계에서의 단위벡터
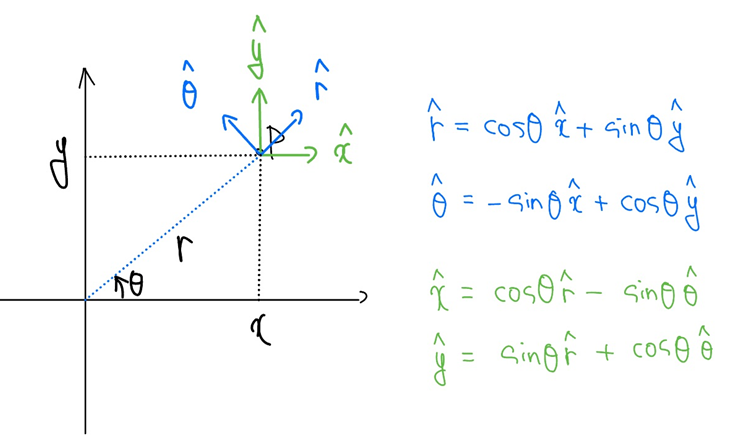
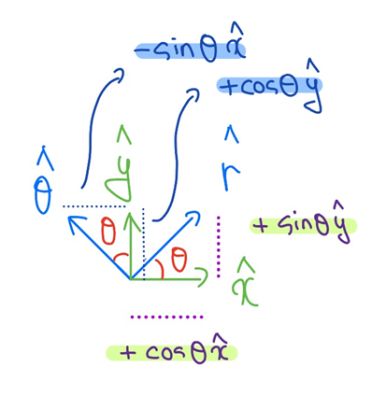
[그림 5]와 같이 평면 상에서 직각좌표계와 극좌표계의 단위벡터는 서로 상대의 단위벡터로 계산이 가능하다.
직각좌표계 단위벡터로 적은 극좌표계 단위벡터
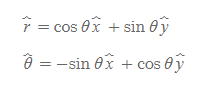
극좌표계 단위벡터로 적은 직각좌표계 단위벡터
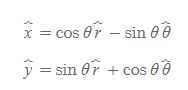
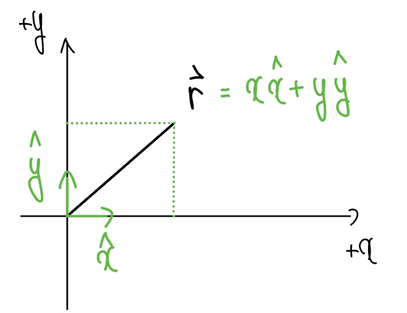
직선, 평면 좌표계에서의 벡터
Vectors on a Line and Plane
1차원의 직선 좌표계에서 (1)위치벡터, (2)변위벡터, (3)속도벡터, (4)가속도벡터를 구해보자. x축의 1차원을 가정하면 각각의 값은 아래와 같다.

2차원 직각좌표계[그림 6]의 4가지 벡터를 구해보자.
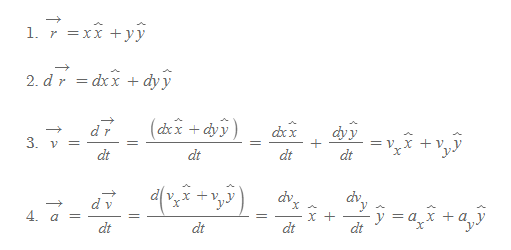
직각좌표계에서 속도의 성분은 x성분은 x좌표만으로, y성분은 y좌표만으로 그 값이 정해진다.
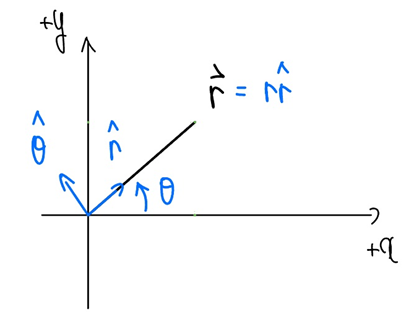
한편 2차원 극좌표계[그림 7]의 4가지 벡터는 다음과 같이 구한다.
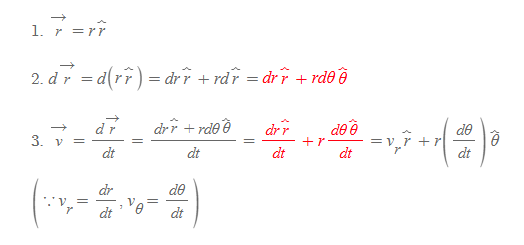
극좌표계에서의 가속도 벡터는 속도벡터를 시간으로 미분하여 구할 수 있다.
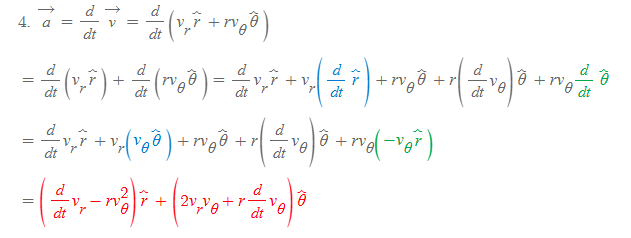
가속도벡터를 구할 때 단위벡터의 미분 계산이 자주 나오는데, 아래에서 극좌표계의 단위벡터 미분식을 구하는 절차를 확인하자. 우선 극좌표계의 단위벡터를 미분하기 위한 사전 지식은 다음과 같다.
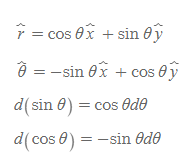
다음 단위벡터 r과 θ의 미분식을 구한다.
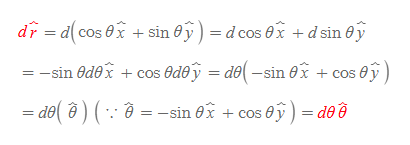
같은 식으로 dθ를 풀면,
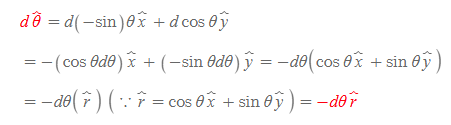
이 된다.
'수학 > 물리학을 위한 수학' 카테고리의 다른 글
| 【물리학을 위한 수학】 05. 벡터미적분학 - 델(나블라) 연산자 (0) | 2025.11.21 |
|---|---|
| 【물리학을 위한 수학】 04. 좌표변환 - 3차원 좌표계 (0) | 2025.11.19 |
| 【물리학을 위한 수학】 03. 원운동 해석 (0) | 2025.11.18 |
| 【물리학을 위한 수학】 01. 기준계와 좌표계 (0) | 2025.11.16 |
| 【미분방정식】 Chapter 1. 변수분리형 방정식 (0) | 2024.10.28 |





