장 이론
장(field)
- 정의 1: 공간에서의 위치, 시간 등에 따라 그 성질을 달리하는 물리량
- 정의 2: 공간의 모든 점에서 정의되는 물리량으로 어떠한 물리량 f가 일정한 공간영역에 걸쳐 그 공간 내의 위치함수로 주어졌을 때의 해당 영역 ⇒ 공간 자체를 물리적 실체로 간주하는 내용으로 영국의 물리학자인 패러데이(Michael Faraday, 1791~1867)가 전기와 자기를 연구하면서 역선의 개념을 도입하면서 시각적으로 이해되기 시작했다.
· 스칼라장(scalar field): 스칼라량 위치함수 영역, 공간 내의 각 점이 크기를 나타내며 분포함 e.g. 온도장, 밀도장, 압력장 등
· 벡터장(vector field): 벡터량 위치함수 영역, 공간 내의 각 점이 크기와 방향을 갖는 벡터를 나타내며 분포함 e.g. 속도장, 중력장, 전기장, 보존력장(퍼텐셜함수) 등

전기장(electric field)은 원천 전하(source charge)인 대전체의 주변 공간영역에 존재한다. ⇒ 전기장은 원천 전하를 원점으로 주변에 퍼져 존재하는데, 이때 전기장을 생성한 전하에 대해서는 공간적으로 어떤 영향(상호작용)도 끼치지 않는다고 전제한다.
시험전하(test charge): , 원천전하에 의해 영향을 받는 존재(전하)로, 전기장에 놓인 test charge는 다음과 같은 특징을 갖는다.
1. 전기장에 포함된 시험전하는 대전체로서 전기력의 효과를 갖는다.
2. 전기장은 벡터량으로 공간 속 한 점의 전기장 벡터는 로 표기한다.
3. 한 점에 놓인 시험전하()는 에 의해 전기력 의 효과를 가진다.

시험전하도 전기장을 형성하지만 전기장의 정의에서는 이 요소는 고려하지 않는다. ⇒ 검출기로서 역할
- 자기 자신이 만든 전기장이 다시 원천(source)에게 영향을 끼칠 수 없다.


이때, F_e는 쿨롱의 법칙의 벡터식으로,
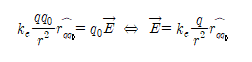


양전하/음전하 전기장 방향
[출처: Wikimedia]

- 의미: 전기장은 전기력과 마찬가지로 벡터합(resultant)으로 표현할 수 있다.
연속전하분포
연속전하분포(continuous charge distribution): 수많은 전하 사이의 거리가 전기장을 구하고자 하는 점(P)까지의 거리에 비해 매우 가까운 경우의 연속적인 전하체
- Δq: 전하체의 작은 전하요소(미소전하요소, charge element)
미소전하요소가 모인 전하체의 총 전기장은 시그마 기호()를 이용해 다음과 같이 표현할 수 있다.

전하분포가 연속적이므로 인 극한에서 P의 전기장은 다음과 같이 계산된다.


- 의미: 연속전하분포의 총 전기장으로, 적분구간은 전체 전하분포영역이다.
전하는 선, 면 및 부피에 분포할 수 있으므로, 전하밀도(charge density)의 개념을 사용하는 것이 편하다.

전하가 부피, 면 혹은 선에 따라 균일하게 분포하지 않은 경우, 미소 전하량은 다음과 같이 정리할 수 있다.
1. 부피미소전하량: dq=ρdV
2. 표면미소전하량: dq=σdA
3. 선미소전하량: dq=λdl
전기력선
전기력선의 특징
- 전기력선(electric line of force): 전기장의 힘을 나타내는 가상의 선
- 전기선속(flux of electric field intensity): 전기력선 다발 또는 집합
1. 전기장 벡터는 각 점에서 전기력선의 접선 방향과 같다.
2. 전기력선의 방향은 전기장 내에 놓인 양의 시험전하가 받는 힘의 방향이다.
3. 전기력선에 수직인 면을 통과하는 단위 넓이 당 전기력선 수는 영역 내 전기장의 크기에 비례한다.
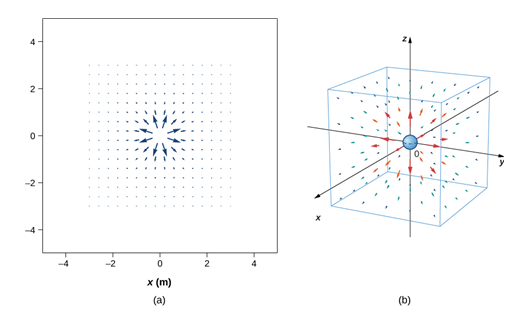
양전하에 의한 공간의 전기력선
[University Physics Volume 2, OpenStax, 2016, p.213]
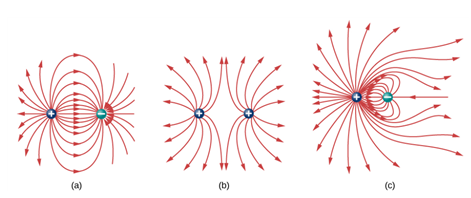
다양한 전기력선의 양상
[University Physics Volume 2, OpenStax, 2016, p.216]
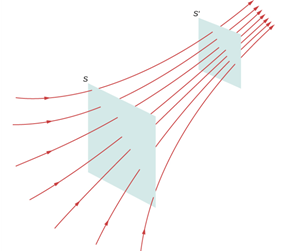
전기력선이 통과하는 가상의 면
[University Physics Volume 2, OpenStax, 2016, p.215]

전기력선 그리기
전하로부터 뻗어나가는 전기력선은 크게 ‘3가지의 그리기 규약’을 만족해야 한다.
1. 전기력선은 양전하에서 시작해 음전하로 끝난다.
2. 전기력선의 수는 전하의 크기에 비례한다.
3. 두 전기력선은 서로 교차할 수 없다.