벡터와 스칼라
벡터(vector): 크기 뿐만 아니라 방향을 고려한 수학적 양
- 스칼라(scalar)는 크기만의 1차원적 양인 반면, 벡터는 2차원의 원소(요소)들에 의해 어떤 양을 표현한다.
- 벡터로 표현될 수 있는 물리량을 벡터량(vector quantity)이라 하며, 벡터량으로는 변위, 속도, 가속도가 있다.

그림 1. 벡터의 표현
- 벡터는 화살표를 그어 표시하며, 벡터 크기는 벡터의 길이로, 벡터 방향은 화살표의 머리(head)로 나타낸다.
- 벡터의 크기와 방향을 바꾸지 않는다면, 벡터를 어디로 위치시키든 벡터 고유의 값은 바뀌지 않는다.

그림 2. 변위
[그림 2]는 변위벡터로 벡터의 가장 간단한 예중 하나이며, 물체의 움직임이 아닌 움직임의 효과를 표현한 것이다.
- 변위벡터는 물체의 최소 이동거리의 크기 값을 갖는다.
- 물체의 실제 이동경로와 달리, 변위벡터는 첫 이동방향을 기준으로 방향이 변하지 않는다. ⇒ 일정한 방향 값을 갖는다.
벡터 더하기

그림 3. Resultant
벡터합(resultant): 두 벡터 또는 그 이상의 벡터를 더한 결과
벡터합

■
- [그림 3]에서 resultant는 벡터 R로 표현된다.
- 2차원에서 두 벡터의 덧셈 방법(resultant 작도법)
[1] 크기와 방향에 맞추어 벡터 a를 그린다.
[2] 벡터 a의 머리부분(head)에 벡터 b의 꼬리부분(tail)이 오도록 벡터 b를 그린다.
[3] resultant는 벡터 a의 꼬리에서 벡터 b의 머리를 잇는 벡터이다.
벡터합의 성질
1. 교환법칙(commutative law) 성립

2. 결합법칙(associative law) 성립


그림 4. 음의 벡터
3. 음의 벡터
- 음의 벡터: [그림 4]에서 벡터 B와 크기는 같으나 방향이 반대인 벡터 C와 같은 경우를 음의 벡터라고 한다.
- 음의 벡터의 성질: 음의 벡터를 더하는 것은 같은 크기의 양의 벡터를 빼는 것과 같다.

같은 크기의 서로 다른 부호의 벡터를 더하면 영벡터(zero vector)가 되는데, 영벡터는 크기와 방향이 모두 없으므로 사실상 0과 같다.

그림 5. Vector Subtraction
벡터 빼기

■
[1] 마이너스 부호가 들어간 벡터는 음의 벡터로 처리할 수 있다.
[2] 음의 벡터는 양의 벡터에 방향만 정반대인 벡터이다.
[3] 음의 벡터를 그려준 뒤, [그림 3]처럼 resultant 작도법을 해준다.
벡터 성분 Components of a Vector

그림 6. Components of a Vector
벡터 성분(vector component): 좌표축에 벡터를 투영시킨 값 [그림 6]
- 스칼라 성분: 벡터 성분의 스칼라량(크기)
- 벡터 성분 그리기(벡터의 분해) [그림 7]
[1] xy-좌표(xy-coord.) 그리기
[2] 벡터의 끝에서 좌표축에 수직한 직선을 그린다. ⇒ vector component를 투영 벡터(projection vector)라고도 한다.
[3] projections: x축에 대한 projection은 x-vector component(projection), y축에 대한 projection은 y-vector component라고 한다.
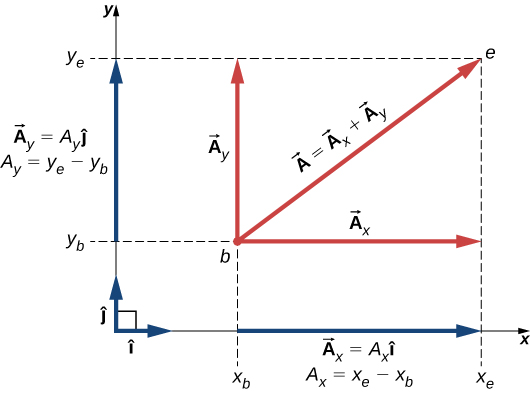
그림 7. 벡터의 분해
projection의 특징
1. 벡터가 놓인 좌표축의 방향선과 정확하게 평행한다.
2. xy-coord.에서 x축의 오른쪽과 y축의 위쪽(북쪽) 방향을 일반적으로 양의 값으로 둔다. 따라서 x축의 왼쪽과 y축의 아래쪽(남쪽) 방향에 projection이 그려지는 경우, 이 vector의 component값은 음의 값이다.
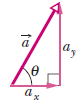
그림 8
성분 찾기
vector와 vector component는 [그림 8]과 같이 직각삼각형을 이루는데, 직각삼각형의 성질을 이용하여 scalar component의 값을 계산할 수 있다.
Scalar Component

■
- 한 벡터의 머리(head)를 다른 벡터의 꼬리(tail)에 연결하여 얻어진 직각삼각형의 빗변(hypotenuse)이 바로 분해 전 원벡터(original vector)이다.
- 벡터 a는 a와 θ로 완벽하게 결정되고, scalar component로도 표현할 수 있다.
Component Notation
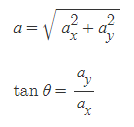
■
단위벡터
단위벡터(unit vector): 크기가 1이며, 특정한 방향을 갖는 벡터 [그림 9]
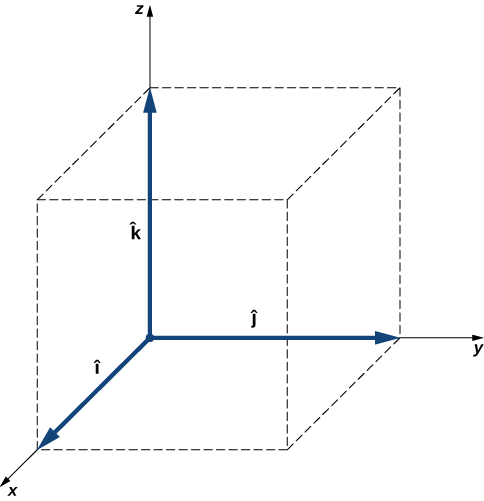
그림 9. Unit Vectors
- unit vector는 축방향과 같다.
- 직각좌표계에서 x, y, z축의 양의 방향을 향하는 단위벡터는,

이다.
- unit vector를 일반 벡터와 구분하기 위하여 화살표가 아닌 hat(^) 기호를 사용한다.
벡터의 표현
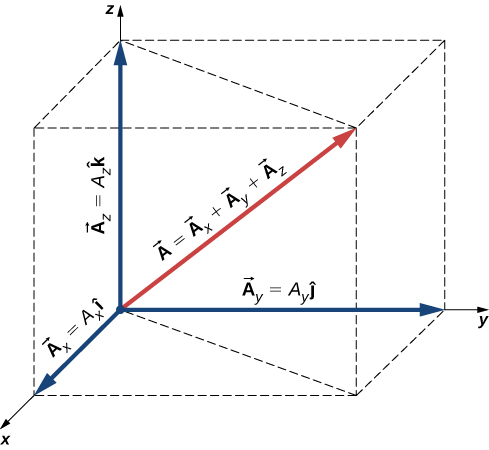
그림 10. 벡터의 표현
[그림 10]과 같은 벡터를 단위벡터를 이용하여 다음과 같이 표현할 수 있다.
벡터표현

■
- Vector Components Vs. Scalar Components(Simply called Components)

벡터성분으로 벡터 더하기
임의의 벡터합이 2차원 상에서 다음과 같은 식을 만족한다고 하자.
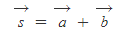
식은 벡터 s가 벡터(a+b)와 서로 같다는 의미로, 이를 만족하기 위해서는 반드시 벡터 s의 대응성분이 벡터(a+b)의 대응성분과 일치해야 한다.
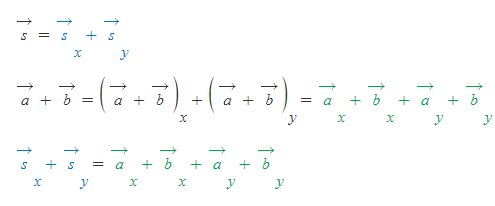
위의 벡터 식에서 x축 성분과 y축 성분을 묶어주면,
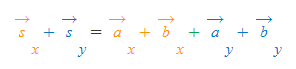
이고,
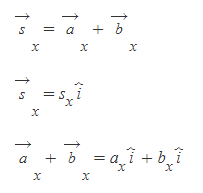
로 내용을 풀 수 있다.
벡터성분으로 벡터 더하기
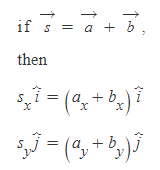
■
두 벡터의 대응성분이 서로 같다면, 두 벡터는 서로 같다.

