[물리학-고전역학] 질량 중심 | Center of Mass

 

질량중심(center of mass): 질점계의 모든 질량이 모인 곳(위치)

• 부피를 갖는 물체의 운동 묘사는 복잡하므로, 이를 단순화 시키기 위해 도입한 관념적 존재 ⇒ 질량 중심은 상황에 따라 물체가 차지한 공간의 밖에 위치할 수도 있음
• 힘에 의한 시스템 전체의 움직임은 계의 '질량 중심'에만 알짜힘이 작용한 효과와 같다.
• 고전역학에서 전체 계(a whole body of the system)는 마치 알짜 외력이 질량 중심인 단일 입자(a single particle of the system)에만 작용한 것처럼 움직인다. ⇒ 역학에서 입자모형을 사용하는 본질적인 이유
• 계의 질량중심 위치는 계의 질량평균위치(average position of the system's mass)이다.

​

「The center of mass is the point at which we can imagine all the mass of an object to be concentrated.」 (Bauer, p.232)

​

질량중심위치와 힘작용위치

 

그림 1

 

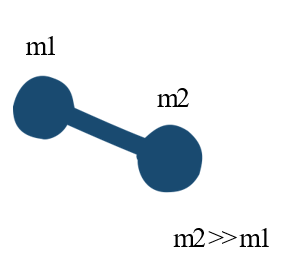
평면에 놓인 아령형의 입자의 두 질량이 [그림 1]과 같이 서로 다를 때, 질량 중심은 아령의 중심으로부터 무게가 '무거운 쪽'으로 쏠려 있다. 즉, m_2가 m_1보다 질량이 클 때 질량 중심은 m_2쪽으로 그 위치가 가깝다.

• 힘이 질량중심보다 위에 작용하면 계는 시계방향으로 회전한다.
• 힘이 질량중심보다 아래에 작용하면 계는 반시계방향으로 회전한다.
• 힘이 질량중심에 작용하면 계는 회전하지 않고 오로지 힘의 방향으로만 움직인다(직선운동을 한다).

​

외력을 가했을 때, 회전의 방향성이나 직선 움직임을 보고 계의 질량중심을 정성적으로 파악할 수 있다.

​

질량중심

..​​

 

■

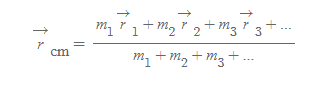
• 물리량

1. r_cm: 시스템의 질량중심 (위치벡터)
2. 각각의 입자에 대한 위치벡터와 질량 값이 사용됨

• 단위: [m]

​

만약 위의 식을 적용하여 물분자[그림 2]의 질량중심을 다음과 같이 구할 수 있다.

 

그림 2

 

 

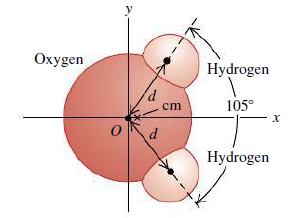
[1] 물 분자는 3개의 원자로 이루어진 계이며, 산소(oxygen)는 16.0u, 수소(hydrogen)는 1.0u의 질량을 갖는다.

[2] 산소 원자의 중심을 O(0, 0)으로 잡는다. 그리고 산소와 붙은 수소에 대해 핵간 거리가 d만큼 떨어졌다 했을 때, d는 대략 10^-10[m]이다. 또한 수소와 산소는 평면 상에서 각각 52.5도의 각도를 갖는다.

[3] 물 분자는 평면 상에서 [그림 2]와 같이 놓이며, x, y축 상의 질량중심을 다음과 같이 구할 수 있다.

 

 

​

​

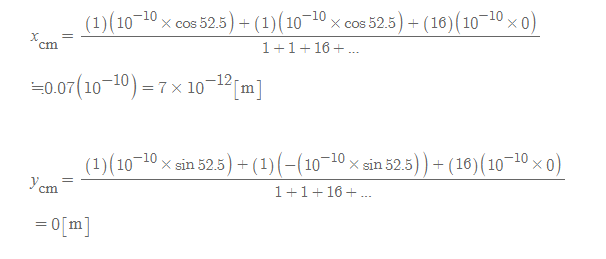
따라서 물 분자의 질량 중심은 다음과 같이 정리할 수 있다.

​

 

그림 3. 다양한 물체의 질량 중심 [출처: Sears & Zemansky's University Physics with Modern Physics, Young & Freedman, 14th ed., 2016, p.279]

 

 

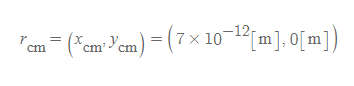
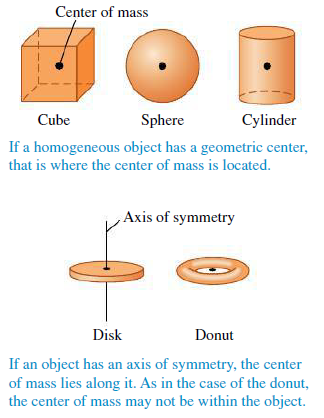
다양한 물체의 질량 중심은 [그림 3]과 같이 나타난다.

​

비대칭적 크기를 가진 물체의 질량중심

우리 주변의 물체는 연속적이고 비대칭적인 질량 분포를 가진다. 하지만 그런 부피를 가진 물체일지라도 극미(infinitesimal)한 정육면체의 연속(continuity)으로 간주할 수 있다.

​

 

그림 4. [출처: Principles of Physics, Serway & Jewett, 12th ed., 2012, p.256]

 

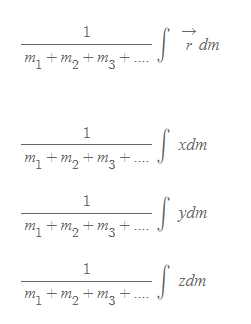
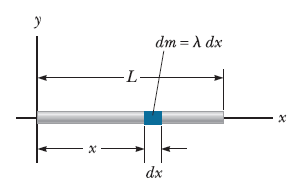
[그림 4]와 같은 L의 길이를 가진 막대기의 질량중심은 다음과 같이 구할 수 있다.

[1] 일정한 선밀도 λ=M/L를 가진 질량 M의 막대기로 가정하고, 이 막대기의 양 끝단을 x축에 놓을 수 있다.

[2] 밀도가 일정한 물체에 대해, 질량이 균일하고 대칭적인 물체의 질량 중심은 대칭축과 대칭면 위에 놓인다.

[3] [과정 1]의 선밀도와 적분식을 활용한 질량중심 식을 사용한다.

 

​

 

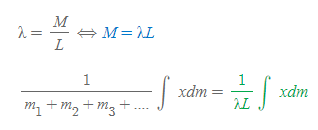
[4] 막대의 전체 질량 M에 대해 막대의 전체 길이 L이 대입되었고, 선밀도는 일정하다고 했기 때문에, 미소 길이 dx와 dm에 대해서도 다음과 같은 식이 성립한다.

 

 

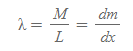
[5] [과정 4]로부터 dm을 유도할 수 있다.

 

 

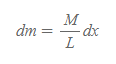
[6] [과정 3]의 초록색 식 dm에 [과정 5]의 결과를 대입한다.

 

​​

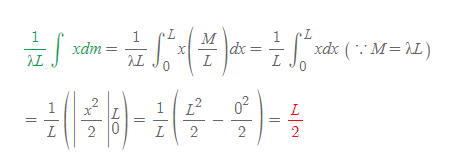
즉, 밀도가 일정한 막대기의 무게 중심은 막대기의 절반 길이에 있다.