벡터와 좌표계 | Vectors and Coordinate Systems

 

벡터 대수

Vector Algebra

 

스칼라(scalar): 크기로 규정되는 양으로 전자기학에서 스칼라량은 대표적으로 전하와 전압이 있다.

벡터(vector): 크기와 함께 방향 또한 함께 고려해야 하는 양으로 전자기학에서 벡터량은 대표적으로 전기장, 자기장이 있다.

• 벡터는 기하학적으로 방향을 나타내는 선분인 화살표[그림 1]로 나타난다.

 

그림 1. 벡터 A

 

• 벡터의 방향은 화살표의 머리이다. 한편 크기는 화살표의 길이와 같다.
• 벡터의 위치만 옮기는 평행이동의 경우, 벡터량은 달라지지 않는다.

​

[그림 2]에서 벡터 A의 성분(components) 및 벡터 A는 다음과 같이 표현 가능하다.

그림 2. 데카르트 좌표계에서의 벡터 A의 표현 [출처: University Physics with Modern Physics, Bauer & Westfall, 2nd ed., 2014, p.24]

$\overrightarrow{A}=\left(A_x,\ A_y\right)\ 또는\ <A_x,\ A_y>$A=(Ax​, Ay​) 또는 <Ax​, Ay​>​

$A_x=\overrightarrow{PQ}=\left(3-\left(-2\right),\ 1-\left(-3\right)\right)=\left(5,\ 4\right)$Ax​=PQ=(3−(−2), 1−(−3))=(5, 4)​

​

벡터 덧셈

두 벡터의 덧셈 A+B는 기하학적으로 A의 머리에 B의 꼬리를 붙이는 방식[그림 2]으로 구할 수 있다.

그림 2. 삼각형법

혹은 [그림 3]과 같이 평행사변형법을 사용해도 된다.

 

그림 3. 평행사변형법

두 가지의 두 벡터의 덧셈법은 그 결과가 서로 일치한다.

• 벡터의 덧셈은 교환법칙(commutative)과 결합법칙(associative)이 성립한다.

$\overrightarrow{A}+\overrightarrow{B}=\overrightarrow{B}+\overrightarrow{A}$A+B=B+A​

$\left(\overrightarrow{A}+\overrightarrow{B}\right)+\overrightarrow{C}=\overrightarrow{A}+\left(\overrightarrow{B}+\overrightarrow{C}\right)$(A+B)+C=A+(B+C)​

스칼라 곱셈

1. 어떤 벡터에 스칼라량 a를 곱하면 그 벡터의 크기는 a배가 된다.
2. a>0인 실수이면, 그 벡터의 방향은 바뀌지 않는다. 하지만 반대의 경우(a<0)인 경우, 그 벡터의 방향은 바뀐다.
3. 스칼라 곱셈(multiplication of a vector by a scalar, scalar multiplication)은 분배법칙(distributive)이 성립한다.

$a\left(\overrightarrow{A}+\overrightarrow{B}\right)=a\overrightarrow{A}+a\overrightarrow{B}$a(A+B)=aA+aB​

4. 어떤 벡터를 스칼라 나눗셈 함은 그 벡터에 스칼라량 a의 역수 1/a를 곱하는 것과 같다.

$\overrightarrow{A}\div a=\overrightarrow{A}\times \frac{1}{a}=\frac{\overrightarrow{A}}{a}$A÷a=A×1a​=Aa​​

​

특히 4번의 성질을 이용하여, 벡터 A를 자신의 크기 A로 나누면 길이가 1이면서 방향은 A와 같은 벡터가 결과 값으로 나타나는 데, 이를 단위 벡터(unit vector)라 정의한다.

 

그림 4. 2차원, 3차원 상의 단위벡터 [출처: University Physics with Modern Physics, Bauer & Westfall, 2nd ed., 2014, p.27]

​

단위 벡터 | Unit Vector

$\hat{a}=\frac{\overrightarrow{A}}{A}$^a=AA​​

■

• 단위벡터의 크기는 1이다.
• 단위벡터의 방향은 그 벡터 A의 방향과 같다.

스칼라곱과 벡터곱

Scalar Product and Vector Product

벡터를 곱하는 방법은 크게 두 가지 종류가 있다.

1. 스칼라곱(scalar product): 점곱(dot product), 벡터 A에 대한 벡터 B의 사영[그림 4]을 곱한 값으로 결과는 스칼라량이다.

그림 4. 벡터 A에 대한 벡터 B의 사영(Acosθ)

점곱은 다음과 같이 정의 된다.

​

Scalar Product(Dot Product)

$\overrightarrow{A}\cdot \overrightarrow{B}\equiv AB\cos \theta _{AB}\ \left(\because \theta _{AB}는\ 벡터\ A,\ B의\ 사잇각\right)$A·B≡ABcosθAB​ (∵θAB​는 벡터 A, B의 사잇각)​

■

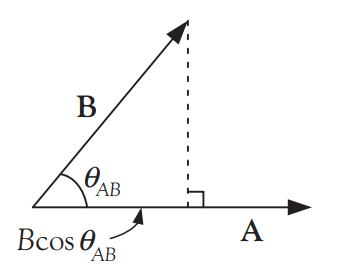
그림 5. Dot Product

기하학적으로 점곱 AB[그림 5]는 벡터 A의 크기에 벡터 B의 벡터 A 방향성분 Bcosθ을 곱한 것과 같다.

• θ이 0도에서 90도 사이인 경우 cosθ는 양수이고, 따라서 점곱은 양의 값을 갖는다.
• θ이 90도에서 180도 사이인 경우 cosθ는 음수이고, 따라서 점곱은 음의 값을 갖는다.
• θ이 90인 경우 cos90=0이므로, 점곱은 0이 된다. ⇒ 수직인 두 벡터의 dot product는 언제나 0이다.

​

점곱의 성질

1. 점곱은 교환법칙이 성립한다.
2. 점곱은 분배법칙이 성립한다.

$\overrightarrow{A}\cdot \left(\overrightarrow{B}+\overrightarrow{C}\right)=\overrightarrow{A}\cdot \overrightarrow{B}+\overrightarrow{A}\cdot \overrightarrow{C}$A·(B+C)=A·B+A·C​

단위벡터의 점곱

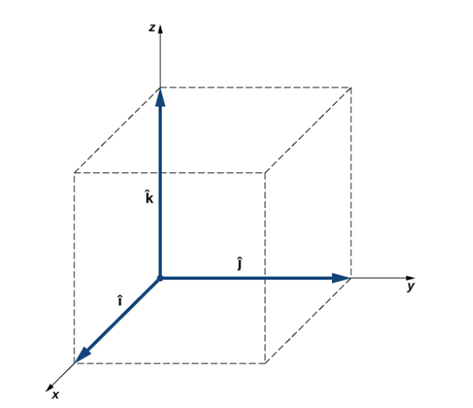
그림 6. 3차원 상의 단위벡터

3차원 상에서 단위벡터는 [그림 6]과 같이 나타나며 이들을 서로 스칼라곱한 결과는 다음과 같다.

$\hat{i}\cdot \hat{i}=\hat{j}\cdot \hat{j}=\hat{k}\cdot \hat{k}=1$^i·^i=^j·^j=^k·^k=1​

$\hat{i}\cdot \hat{j}=\hat{j}\cdot \hat{k}=\hat{k}\cdot \hat{i}=0\ \left(\because \hat{i}\rightanglearc \hat{j}\rightanglearc \hat{k}\right)$^i·^j=^j·^k=^k·^i=0 (∵^i⊾^j⊾^k)​

• 단위벡터의 스칼라곱에서 윗 내용은 사잇각 θ이 0인 것으로 서로 평행하는 경우 scalar product의 결과는 다음과 같다.

$\overrightarrow{A}\cdot \overrightarrow{A}=A^2$A·A=A2​

단, 단위벡터의 크기는 1이므로 1을 제곱해도 역시 1이 나오기 때문에 위와 같은 결과가 성립된다.

​

• 단위벡터의 스칼라곱에서 아래 내용은 사잇각 θ이 90인 것과 정확히 일치한다.

​

2. 벡터곱(vector product): 가위곱(cross product), 벡터 A, B를 가위곱하면 그 결과 값은 벡터량[그림 7]이다.

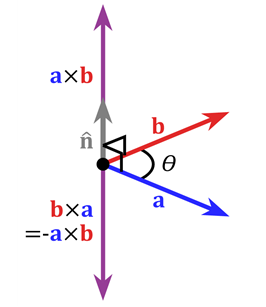
그림 7. 벡터곱 [출처: Wikimedia]

Vector Product(Cross Product)

$\overrightarrow{A}\times \overrightarrow{B}=\hat{a}_nAB\sin \theta _{AB}\ \left(\because 0\le \theta _{AB}\le 180\right)$A×B=^an​ABsinθAB​ (∵0≤θAB​≤180)​

■

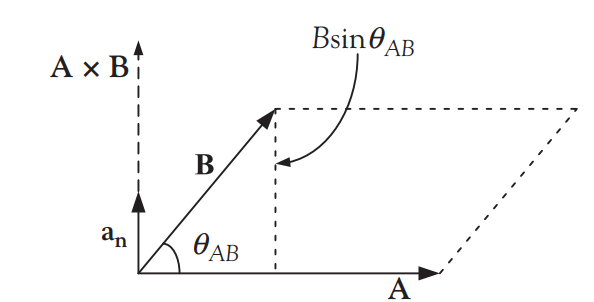
그림 8. 두 벡터의 가위곱

vector product 식의 물리량은 [그림 8]을 통해 확인할 수 있다.

• 벡터 A, B의 cross product 크기는 ABsinθ_AB이다. 즉, 벡터 A와 B가 만드는 평행사변형의 면적과 정확히 일치한다.
• 단위벡터 a_n은 가위곱의 방향으로 평행사변형이 놓인 평면에 수직한다. a_n의 방향은 [그림 9]와 같이 오른손 규칙으로도 확인할 수 있다.

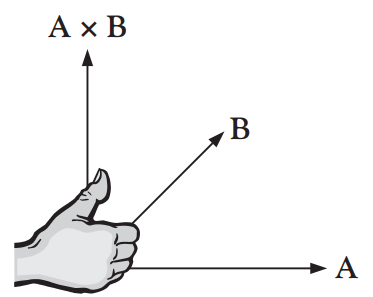
그림 9. 가위곱의 방향

가위곱의 성질

1. 가위곱은 분배법칙이 성립한다.
2. 가위곱은 교환법칙이 성립하지 않는다. 대신 역교환법칙을 따른다.

$\overrightarrow{A}\times \overrightarrow{B}=-\overrightarrow{B}\times \overrightarrow{A}$A×B=−B×A​

3. 가위곱을 하는 두 벡터 A, B의 사잇각이 90도일 때, sin90=1이므로 최대 크기 AB를 갖는다. 반면 두 벡터 A, B의 사잇각이 0도일 때, sin0=0이므로 벡터곱의 크기 또한 0이 된다.

​

단위벡터의 가위곱

단위벡터의 가위곱은 가위곱의 성질에 따라 다음과 같이 정리된다.

$\hat{i}\times \hat{i}=\hat{j}\times \hat{j}=\hat{k}\times \hat{k}=0$^i×^i=^j×^j=^k×^k=0​

$\hat{i}\times \hat{j}=\hat{k}$^i×^j=^k​

$\hat{j}\cdot \hat{k}=\hat{i}$^j·^k=^i​

$\hat{k}\cdot \hat{i}=\hat{j}\ \left(\because \hat{i}\rightanglearc \hat{j}\rightanglearc \hat{k}\right)$^k·^i=^j (∵^i⊾^j⊾^k)​

삼중곱 Triple Product

삼중곱은 두 벡터의 곱과 마찬가지로 그 결과에 따라 2가지 곱이 존재한다.

1. 스칼라삼중곱
2. 벡터삼중곱

​

스칼라삼중곱

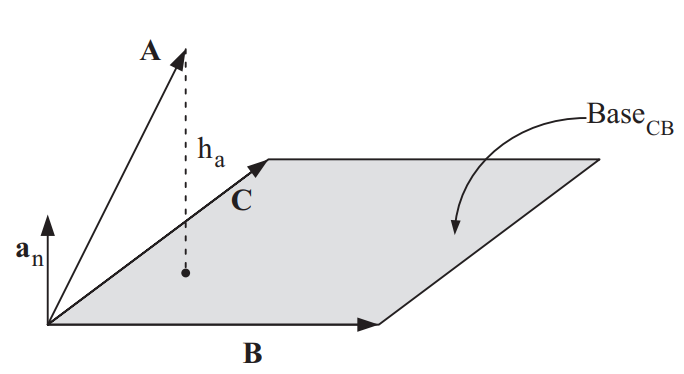
그림 10. 삼중곱

스칼라삼중곱[그림 10]의 결과는 스칼라량으로, 세 벡터가 만드는 평행육면체의 부피와 그 값이 같다.

• 단위벡터 a_n은 벡터 B와 C의 가위곱 방향과 같다. 또한, Base_CB는 벡터 B, C의 가위곱 면적이다.

$\overrightarrow{B}\times \overrightarrow{C}=\hat{a}_n\normal{1}{Base}_{BC}$B×C=^an​BaseBC​​

$$​

$\overrightarrow{A}\cdot \left(\overrightarrow{B}\times \overrightarrow{C}\right)=\textcolor{#0078cb}{\overrightarrow{A}\cdot \hat{a}_n}\normal{1}{Base}_{BC}$A·(B×C)=A·^an​BaseBC​​

$$​

$\textcolor{#0078cb}{\overrightarrow{A}\cdot \hat{a}_n}=Aa_n\cos \theta _{Aa_n}=\pm h_a$A·^an​=Aan​cosθAan​​=±ha​​

• 만약 벡터 A와 단위벡터 a_n의 사잇각이 90도 미만이면 [그림 10]의 h_a 값은 양수이다. 반면 90도를 초과한다면 h_a 값은 음수이다.
• 벡터 A와 단위벡터 a_n의 스칼라곱의 결과는 평행육면체의 높이 값과 같다. 그리고 이 평행육면체의 부피가 스칼라삼중곱이다.

​

스칼라삼중곱

$\overrightarrow{A}\cdot \left(\overrightarrow{B}\times \overrightarrow{C}\right)=\pm \hat{h}_a\left(\normal{1}{Base}_{BC}\right)$A·(B×C)=±^ha​(BaseBC​)​

■

• 스칼라삼중곱의 점곱, 가위곱 순서를 바꾸어도 결과는 동일하다.

$\overrightarrow{A}\cdot \left(\overrightarrow{B}\times \overrightarrow{C}\right)=\left(\overrightarrow{A}\times \overrightarrow{B}\right)\cdot \overrightarrow{C}$A·(B×C)=(A×B)·C​

벡터삼중곱

벡터삼중곱은 간단하게 결과 값만 확인하자.

​

벡터삼중곱

$\overrightarrow{A}\times \left(\overrightarrow{B}\times \overrightarrow{C}\right)=\overrightarrow{B}\left(\overrightarrow{A}\cdot \overrightarrow{C}\right)-\overrightarrow{C}\left(\overrightarrow{A}\cdot \overrightarrow{B}\right)$A×(B×C)=B(A·C)−C(A·B)​

■

단위벡터와 벡터 성분

Unit Vectors and Components

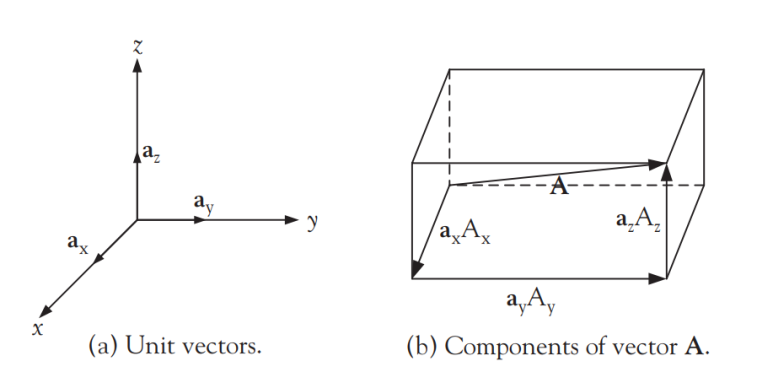
그림 1. 단위벡터와 성분

좌표계를 도입하면 벡터를 성분(components)으로 나타낼 수 있고, [그림 1]은 직각 좌표계(rectangular coordinate system, Cartesian coordinate system)를 사용하여 나타낸 벡터 그림이다.

• [그림 1]의 (a)는 unit vector들로 직각 좌표계의 x, y, z축과 그 방향성이 정확히 일치한다.
• [그림 1]의 (b)는 임의의 벡터 A로 x, y, z축에 각각 투영시킨 정사영벡터(projections)가 함께 그려져 있다. ⇒ 벡터 덧셈에 따라 벡터 A는 projection을 활용하여 아래와 같이 정의된다.

$\overrightarrow{A}=\hat{a_x}A_x+\hat{a_y}A_y+\hat{a_z}A_z$A=^ax​Ax​+^ay​Ay​+^az​Az​​

• 성분벡터 Vs. 성분

3차원 직각 좌표계에서 벡터 A의 성분벡터와 성분은 아래와 같이 정의된다.

$\overrightarrow{A}=\textcolor{#0078cb}{\overrightarrow{A}_x+\overrightarrow{A}_y+\overrightarrow{A}_z}=\textcolor{#00a84b}{A_x}\hat{a}_x+\textcolor{#00a84b}{A_y}\hat{a}_y+\textcolor{#00a84b}{A_z}\hat{a}_z$A=Ax​+Ay​+Az​=Ax​^ax​+Ay​^ay​+Az​^az​​

 

• 파란색은 (벡터 A의) 성분벡터이고, 초록색은 (벡터 A의) 성분이라 한다.

세 가지 좌표계

Three Geometry Coordinate System

전자기학에서 다루는 문제는 3차원의 세상이고, 이를 표현할 수 있는 좌표계는 크게 3가지이다.

1. 직각좌표계(rectangular coordinate system)
2. 원통좌표계(cylindrical coordinate system)
3. 구좌표계(spherical coordinate system)

​

직각좌표계

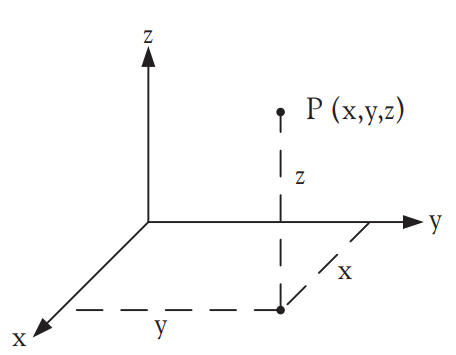
그림 2. 직각좌표계

직각좌표계[그림 2]는 오른손 법칙[그림 3]으로 설정된 좌표축의 시스템이다.

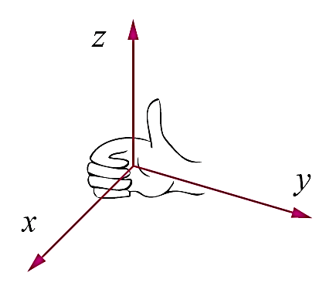
그림 3. 오른손 법칙

• 각각의 축은 x, y, z로 명명되며, 이들의 단위벡터는 i, j, k 또는 hat x, hat y, hat z로 표현한다.
• 원점으로부터 각 축을 향해 뻗어나가는 정도를 x, y, z라고 하면, 점 P는 P(x, y, z)[그림 2]로 표현된다.

​

원통좌표계

 

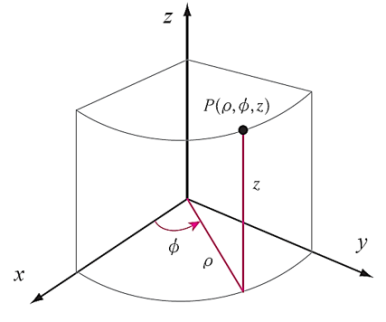
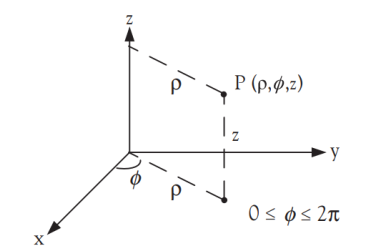
그림 4. 원통좌표계

• 원통좌표계는 직각좌표계의 x, y, z처럼 세 가지의 특수한 좌표값을 갖는다.

1. ρ: (점 P가) z축으로부터 떨어진 거리[그림 4]
2. φ: 방위각(azimuth angle), +x축으로부터 반시계 방향의 각도
3. z: xy평면으로부터 높이

​

• 각각의 좌표는 아래와 같은 특수한 조건값을 만족해야 한다.

 

$\rho \ge 0$ρ≥0​

$0\le \phi \le 2\pi \ 또는\ -\pi \le \phi \le \pi $0≤𝜑≤2π 또는 −π≤𝜑≤π​

$-\infty \le z\le +\infty $−∞≤z≤+∞​

원통좌표계의 각각의 좌표에 대한 단위벡터는 다음과 같다.[그림 5]

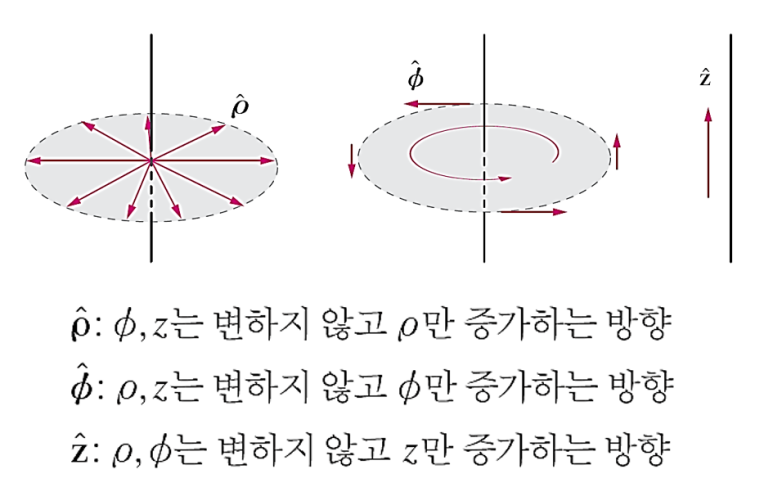
그림 5. 원통좌표계 단위벡터의 설명 [출처: Able 전자기학]

원통좌표계의 단위벡터는 방사(ρ), 회전(φ), 그리고 증가(z)의 형태를 보인다.

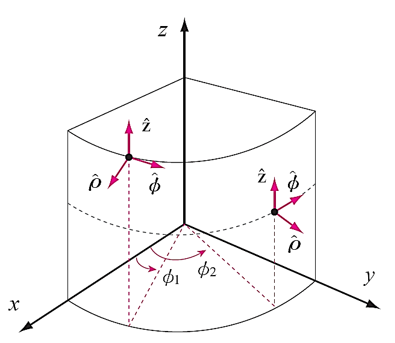
그림 6

• 원통좌표계의 각 단위벡터는 [그림 6]과 같이 서로 수직한다. 특히 단위벡터 ρ와 φ는 φ좌표의 함수이다.
• 원통좌표계의 기본단위벡터를 활용하여, 각 성분의 크기를 가진 벡터를 아래와 같이 표현할 수 있다.

$\overrightarrow{A}=A_{\rho }\hat{\rho }+A_{\phi }\hat{\phi }+A_z\hat{z}$A=Aρ​^ρ+A𝜑​^𝜑+Az​^z​

직각좌표계와 원통좌표계의 변환

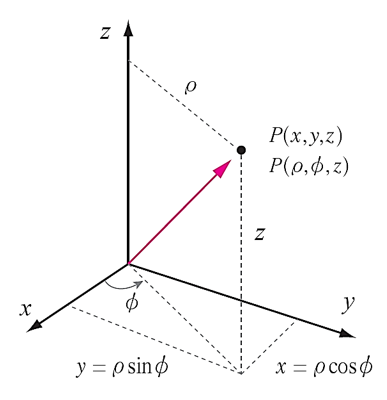
그림 7. 직각좌표계와 원통좌표계

3차원의 좌표 시스템에 놓인 점 P는 직각 좌표계와 원통 좌표계 모두의 좌표값으로 표현될 수 있으며, 이들은 서로 변환되어 계산될 수 있다.[그림 7]

• 원통 → 직각: 원통좌표를 이용하여 직각좌표를 구하는 식

$x=\rho \cos \phi $x=ρcos𝜑​

$y=\rho \sin \phi $y=ρsin𝜑​

$z=z$z=z​

• 직각 → 원통: 직각좌표를 이용하여 원통좌표를 구하는 식

$\rho =\sqrt{x^2+y^2}$ρ=√x2+y2​

$\phi =\tan ^{-1}\left(\frac{y}{x}\right)$𝜑=tan−1(yx​)​

$z=z$z=z​

​

구좌표계

 

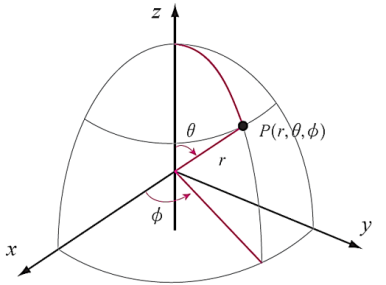
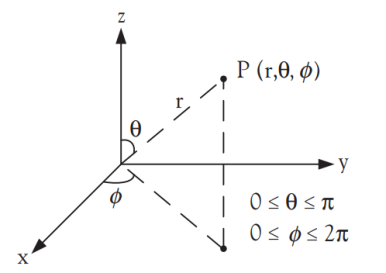
그림 8. 구좌표계

• 구 좌표계[그림 8] 역시 특수한 세 가지 좌표를 갖는다.​

1. r: 원점으로부터 떨어진 거리
2. θ: 편각(polar angle), +z축으로부터의 각도(z축과 선 OP가 이루는 각도[그림 8])
3. φ: +x축으로부터 반시계 방향의 각도

​

• 각각의 좌표는 아래와 같은 특수한 조건값을 만족해야 한다.

$r\ge 0$r≥0​

$0\le \theta \le \pi $0≤θ≤π​

$0\le \phi \le 2\pi \ 또는\ -\pi \le \phi \le \pi $0≤𝜑≤2π 또는 −π≤𝜑≤π​

구좌표계의 기본단위벡터는 [그림 9]와 같은 형태를 갖는다.

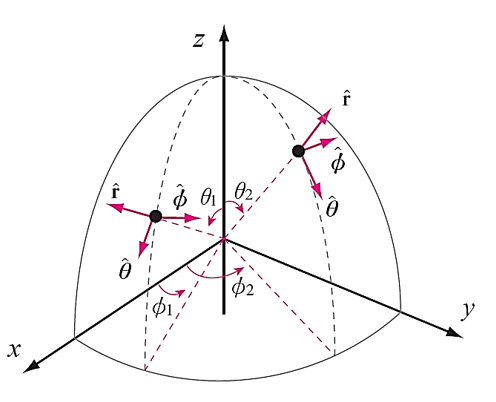
그림 9. 구좌표계의 단위벡터

• 구좌표계의 기본단위벡터를 활용하여, 각 성분의 크기를 가진 벡터를 아래와 같이 표현할 수 있다.

$\overrightarrow{A}=A_r\hat{r}+A_{\theta }\hat{\theta }+A_{\phi }\hat{\phi }$A=Ar​^r+Aθ​^θ+A𝜑​^𝜑​

직각좌표계와 구좌표계의 변환

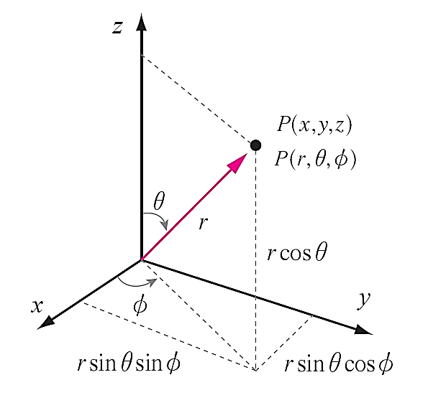
그림 10

직각좌표계를 구좌표계 또는 반대의 좌표 내용으로 변환[그림 10]할 수 있다.

• 구좌표 → 직각좌표: 구좌표를 활용하여 직각좌표를 구하는 식

$x=r\sin \theta \cos \phi $x=rsinθcos𝜑​

$y=r\sin \theta \sin \phi $y=rsinθsin𝜑​

$z=r\cos \theta $z=rcosθ​

• 직각좌표 → 구좌표: 직각좌표를 이용하여 구좌표를 구하는 식

$r=\sqrt{x^2+y^2+z^2}$r=√x2+y2+z2​

$\theta =\tan ^{-1}\left(\frac{\sqrt{x^2+y^2}}{z}\right)$θ=tan−1(√x2+y2z​)​

$\phi =\tan ^{-1}\left(\frac{y}{x}\right)$𝜑=tan−1(yx​)​

원통좌표-구좌표의 직접적인 변환은 그 공식이 비직관적이기 때문에, 대부분 처음 제시된 좌표계의 좌표를 직각좌표로 변환한 뒤 이 변환된 직각좌표를 원통좌표 또는 구좌표로 변환한다.

​

좌표의 변환

Equations of Transformation Between Coordinate Systems

좌표의 변환식을 정리하면 아래와 같다.

​

1. 원통좌표를 이용하여 직각좌표를 구함 식

$x=\rho \cos \phi $x=ρcos𝜑​

$y=\rho \sin \phi $y=ρsin𝜑​

$z=z$z=z​

2. 직각좌표를 이용하여 원통좌표를 구함 식

$\rho =\sqrt{x^2+y^2}$ρ=√x2+y2​

$\phi =\tan ^{-1}\left(\frac{y}{x}\right)$𝜑=tan−1(yx​)​

$z=z$z=z​

• 원통좌표와 직각좌표의 z값은 서로 같다.
• 원통좌표의 ρ는 점 P의 xy평면(2차원) 위의 투영과 원점 사이의 거리이고, 방위각 φ 또한 xy평면(2차원) 상의 각이므로, 둘은 '2차원 상의' 직각좌표와 평면 극좌표(polar coordinate) 간의 관계식과 매우 유사하다.

​

3. 구좌표를 활용하여 직각좌표를 구함 식

$x=r\sin \theta \cos \phi $x=rsinθcos𝜑​

$y=r\sin \theta \sin \phi $y=rsinθsin𝜑​

$z=r\cos \theta $z=rcosθ​

4. 직각좌표를 이용하여 구좌표를 구함 식

$r=\sqrt{x^2+y^2+z^2}$r=√x2+y2+z2​

$\theta =\tan ^{-1}\left(\frac{\sqrt{x^2+y^2}}{z}\right)$θ=tan−1(√x2+y2z​)​

$\phi =\tan ^{-1}\left(\frac{y}{x}\right)$𝜑=tan−1(yx​)​