Herald-Lab
【2022 물리학 | 고전역학】 좌표계와 삼각함수 ☆보충자료☆ 본문

물리학의 여러 가지 문제는 공간상에서의 위치 표현으로부터 시작되고, 이를 위해서는 벡터에 대한 내용을 반드시 숙지해야함을 여러 차례 강조하였다.
- 벡터의 수학적 해석을 위해 삼각법(trigonometry)이 도입되었다.
· trigonometry: 삼각형의 변과 각 사이의 관계에 따른 여러 가지 기하학적 도형을 연구하는 수학의 한 분과
- 공간상의 위치표현은 프랑스의 철학자 르네 데카르트(René Descartes, 1596~1650)가 쓴 저서 『기하학(La Géométrie)』(1637)과 프랑스의 법조인 페르마(Pierre de Fermat, 1607~1665)의 3차원에 관한 연구로부터 발견할 수 있다. ⇒ 특히 데카르트는 직각좌표계를 이용해 유클리드 기하학(Euclidean geometry)과 대수학(algebra)의 혁신적으로 연결했다.
- 좌표계(coordinate system): 물리량의 값(수치)을 공간 상 좌표로 표현하기 위해 도입한 체계, 물체의 운동을 기술할 때 반드시 필요함
· 좌표(coordinates): 좌표계에서 물체의 운동 및 그 위치에 부여된 수치 또는 성분
· 해석기하학에서는 점이 좌표 (x, y, z)로 표현되면서, 도형의 성질을 방정식으로 풀어낼 수 있게 됨
좌표계의 도입
① 점은 coordinates의 실수 순서쌍(ordered pair, ordered set)으로 간주된다.
- 순서쌍이란 순서가 고려되는 둘 이상의 변수로 (a, b)로 흔히 표현된다.
- x, y축(x, y-)의 두 축 시스템(직각좌표계)에서 coordinate (x, y)는 (a, b)로 표현되며, (a, b)≠(b, a)이다.
② 직선, 곡선, 평면은 형태에 따라 방정식으로 표현가능하다.
③ 도형의 성질 또한 방정식의 형태로 설명하고, 방정식의 해(solution)는 기하학적 대상이 된다.
e.g. 반지름이 1인 구는 이다.
좌표계(좌표시스템)
일반물리학 수준에서 좌표계는 2차원 좌표계가 많이 쓰이며, (1)평면직각좌표계와 (2)평면극좌표계가 대표적이다.
데카르트 좌표계(Cartesian coordinate system, 평면직각좌표계): 이차원 상에서 원점(origin) O(0, 0)을 기준으로 서로 수직하는 두 축을 그린 좌표계이다. 임의의 한 점 P는 P(x, y)로 표시한다.
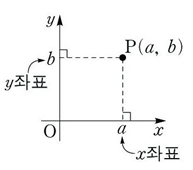
- 좌표평면: x, y-으로 이루어진 임의의 평면
- 좌표평면에서 원, 직사각형, 정사각형, 곡선 등의 모양이 수치적으로 정의된다.
직교좌표계(orthogonal coordinate system): 각각의 축 또는 축평면이 직교성을 유지하는 좌표계
평면 극좌표계(polar coordinate system): 평면 극좌표계는 평면상의 한 점을 표기할 때 (r, θ)를 사용해 점의 위치를 표현할 수 있다. ⇒ 평면 극좌표계의 기원은 고대 그리스의 천문학자 히파르코스(Hipparchus of Nicaea, c. B.C. 190~c. B.C. 120)가 남긴 각도에 따른 현의 기록(a table of chord functions)으로부터 찾을 수 있다.
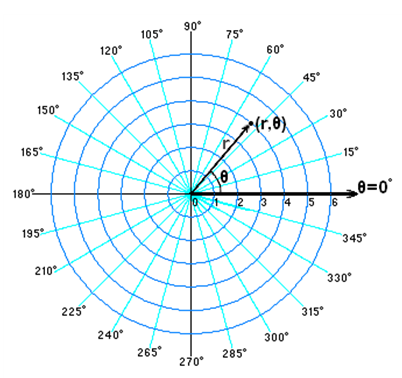
- r: 직각 좌표의 원점으로부터 한 점의 특정 위치인 (x, y)까지의 거리
- θ: 원점에서 주어진 점까지 그은 선분과 고정된 x-사이의 각도
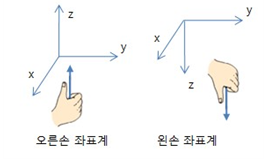
고정 축은 대개 +x-(원점으로부터 오른쪽 x축 구간)을 택하고 각도는 반시계(counter-clockwise) 방향으로 측정한다. ⇒ 오른손을 기준으로 오른손가락을 감싸는 방향을 (+) 방향으로 설정했다.
① +θ: +x-로부터 반시계 방향의 각도
② -θ: +x-로부터 시계 방향의 각도
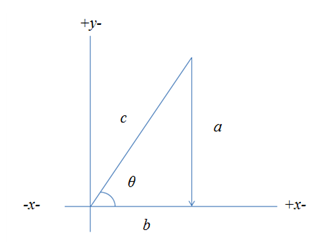
trigonometry의 정보를 이용해 평면 극좌표로부터 직각 좌표계 얻을 수 있다.
- 단, θ를 +x-으로부터 반시계 방향으로 측정된 각으로 정의하는 경우에만 아래 식을 사용할 수 있다.
- 직각삼각형의 변 a는 각도 θ를 전혀 끼지 않은 높이 변(opposite)이고, 변 는 각도에 대해 밑변(adjacent), 변 는 빗변(hypotenuse)이라 한다.
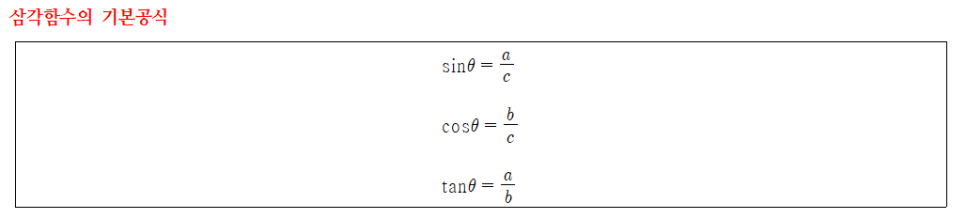
삼각함수(trigonometric functions)란, 각의 크기를 삼각비로 나타낸 함수로 예각 삼각함수는 직각 삼각형의 예각(acute angle)에 직각 삼각형의 두 변 길이의 비를 대응시킨다.
삼각함수의 기본공식을 따르면, tanθ는 다음과 같이 쓸 수도 있다.
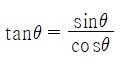
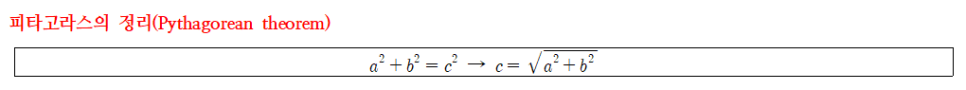
피타고라스의 정리를 활용해 (피타고라스 항등식, Pythagorean identity)이란 식을 유도할 수 있다. ⇒ 삼각함수 항등식을 참고
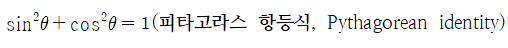
삼각함수
좌표계를 이해하기 위해서는 기본적으로 삼각함수(trigonometric function)를 이해해야 한다. 삼각함수는 직각삼각형의 특수한 성질에 기초한 수학의 한 분야이다.
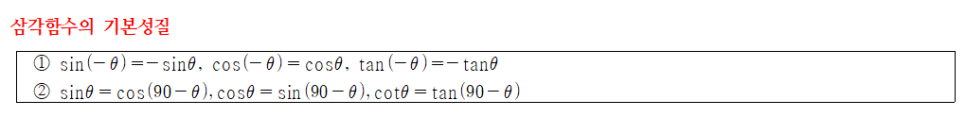
기본성질 이외에도 삼각함수와 연관해 매우 중요한 단서가 되는 식들이 있는데, 아래는 삼각함수의 항등식(trigonometric identity)으로 물리학의 문제를 푸는 데 종종 활용된다.
삼각함수 항등식

직각삼각형이 아닌 삼각형에 대해서는 사인 법칙과 코사인 법칙을 적용한다.
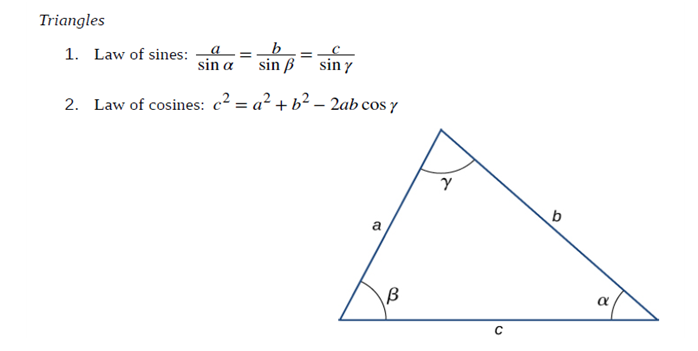
그리고 아래의 삼각함수 공식들도 때에 따라서 잘 활용된다.
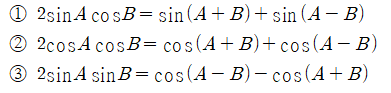
추가로 반각공식도 알아두자.
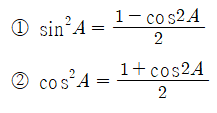
코시컨트, 시컨트, 그리고 코탄젠트
사인, 코사인, 그리고 탄젠트 값은 모두 그에 상응하는 역수 값을 갖는다.

'고급물리학 > 고전역학' 카테고리의 다른 글
| [물리학-고전역학] 질량 중심 | Center of Mass (0) | 2023.10.08 |
|---|---|
| 벡터와 좌표계 | Vectors and Coordinate Systems (0) | 2022.07.01 |
| 【2022 물리학 | 고전역학】 힘의 종류: 마찰력 | 이론 (0) | 2022.01.12 |
| 【2022 물리학 | 고전역학】 힘의 종류: 수직항력 ★문제풀이★ (0) | 2022.01.09 |
| 【2022 물리학 | 고전역학】 뉴턴의 운동법칙: 가속도와 작용-반작용 (0) | 2022.01.08 |





