

미국의 물리학자 밀리컨(Robert Millikan, 1868~1953)은 1909년부터 1913년까지 전자가 가지는 기본 전하량의 크기 e를 측정하는 실험(기름방울 실험, oil-drop experiment)을 수행하여 전자의 전하량이 양자화되었음을 증명했다.
- 그의 지도학생이었던 미국의 물리학자 하비 플레쳐(Harvey Fletcher, 1884-1981)는 자신의 사후 1년 뒤, 기름방울 실험에 대한 '비망록'을 남겼는데, (1)기름방울 실험은 사실 자신이 먼저 고안을 한 것이며, (2)밀리컨이 이 내용을 자신을 단독 저자 논문으로 게재하는 대신, 다른 논문을 단독 저자인 박사 논문으로 트레이드 했다고 전했다.
- 또한 수많은 실험 결과 중 자신에게 유리한 데이터만을 선별한 정황이 있다. 175개의 실험 데이터 중 58개만을 선택적으로 발표하였으며, 따라서 밀리컨의 실험은 현재까지도 연구 윤리를 지키지 않은(데이터 조작) 사례로 자주 언급된다. ⇒ 실험 결과 보고에 있어 부적절한 데이터를 생략할 경우, 그 데이터의 선별에 합당한 이유 또한 반드시 기록되어야 한다.[출처: 2019 여름호 포스테키안, "Science Black Box"]
- 그럼에도 불구하고, 많은 기름방울에 의한 반복적인 측정을 통해 '어떤 기본적인 물리량의 정수배'를 발견하였는데, 이 때 기본 물리량으로 계산된 값은 1.592 (17)×10^-19[C]이었다.

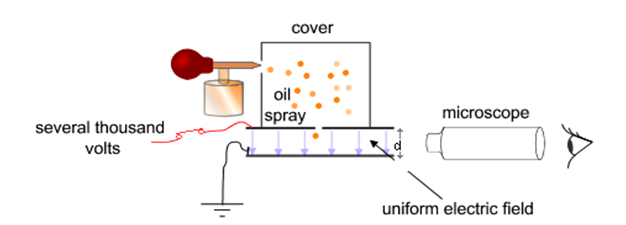
밀리컨의 기름방울 실험 세팅은 [그림 1]과 같이 간략하게 나타낼 수 있다. 장비 및 준비과정은 대략 아래와 같다.
[1] 공기 이온화
- 상자 안에 있는 공기에 X선을 쬐어 먼저 공기를 이온화(ionization)시킨다. ⇒ 이온화란 중성상태의 물질이 어떤 외부 요인으로 인해 특정 전하를 가지게 되는 것을 뜻한다.
- 이온화된 공기로부터 자유전자가 빠져나오고, 이들이 분사한 기름방울에 붙어 기름방울은 음전하를 가지게 된다.
[2] 기름방울
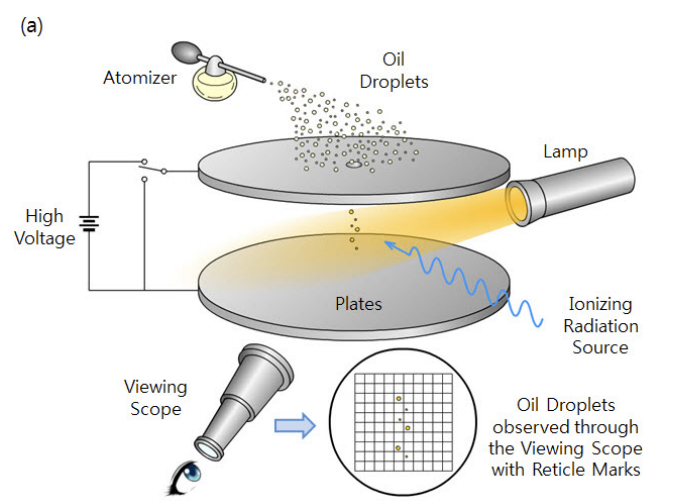
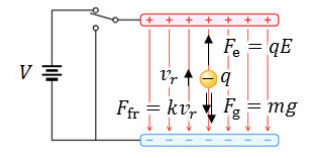
- 두개의 평행 금속판(plates)이 있는 실험장치[그림 2]로, 양단에 전지를 연결하여 전기장을 생성한다.
- 기름을 담은 분무기(atomizer)가 평행판 위에 배치되어 있다. 분무기에서 미세한 기름방울(oil droplets)들이 방출된다.
- 평행판 사이에 미세 구멍이 있어서 분사한 기름방울 중 일부가 금속판 내부로 들어가게 된다.
실험분석
질량이 m이고 전하량이 q인 음전하를 띤 기름방울
[1] 금속판 사이에 전기장이 없는 경우, 전하에 작용하는 힘은 중력(F_g)과 점성항력(F_D)이다.
전기장 부재시, 종단속력에 도달한 기름방울
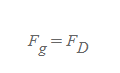
- 첫(1) 번째 상황에서 종단속력에 도달한 기름방울에 가해진 점성항력은 그 속력에 비례해 다음과 같다.
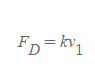
[2] 금속판 사이에 전기장을 거는 경우, 전하에 작용하는 힘은 중력(F_g)과 전기력(F_e), 그리고 점성항력(F_D')이다. 전기장에 의해 기름 방울은 상승하게 되는데, 이 때 점성항력은 상승(+)하는 반대 방향 즉, 중력의 방향(-)과 일치한다. 마찬가지로 이 힘이 균형을 이루어 종단속력에 도달한 기름방울을 통해 아래 식을 세울 수 있다.
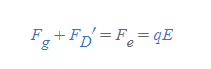
- 두(2) 번째 상황에 종단속력에 도달한 기름방울에 가해진 점성항력은 그 속력에 비례해 다음과 같다.
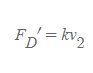
- 전기력의 경우 q가 음전하이고 전기장은 아래로 향하기 때문에, 전기력은 위쪽 방향으로 작용[그림 3]한다. ⇒ 즉, 중력과 반대방향으로 전기력이 작용함을 의미
[3] 물체에 작용하는 중력은 mg, 평형하는 두 도체판에서의 전기장 E=V/d(두 도체판 사이의 거리)임을 적용한다.
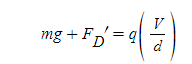
- 두 가지 경우 모두, 공기에 대한 부력이 존재하나, 공기의 밀도는 기름에 비해 매우 미비한 수준이므로, 부력의 값은 무시하도록 한다.
[4] 점성항력이란, 공기의 점성(viscosity)에 의한 점성력(viscous force)으로 (1)반경이 r인 구형 물체가 (2)점도가 η(에타, eta)인 유체에서 (3)속도 v로 이동할 때 아래 크기와 같은 점성항력을 갖는다.
스토크스의 법칙
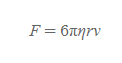
■
- 물리량
- η: 유체의 점도
- v: 유체를 지나는 물체의 속력
- r: 유체를 지나는 물체의 반지름
[5] F_D는 곧 스토크스의 법칙을 적용한 값으로 식을 다시 정리하면,
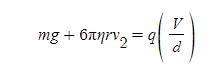
이다.
[6] [과정 1]의 식에도 스토크스의 법칙을 적용한다.
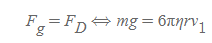
[7] [과정 5]와 [과정 6]의 결과 식에서 6πηr을 소거하고 q에 대해 정리하면 다음 식을 유도할 수 있다.
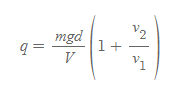
[8] 기름방울이 구형에 밀도 ρ, 반경이 r이면, [과정 7]의 식을 다음과 같이 고칠 수 있다.
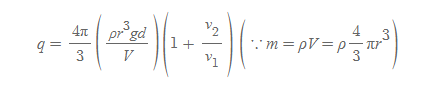
[9] 기름방울의 질량 m 식과 스토크스의 법칙을 조합하면, 기름 방울의 반지름 r을 구할 수 있고, 이를 [과정 8]의 식에 대입하면 최종적으로 q를 구할 수 있다.
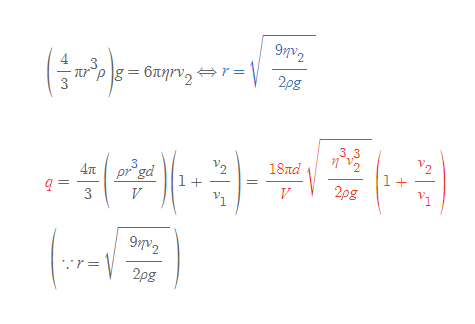
'고급물리학 > 전자기학' 카테고리의 다른 글
| [물리학-전자기학] 16. 저항과 옴의 법칙 | Electrical Resistance and Ohm's Law (0) | 2023.10.12 |
|---|---|
| [물리학-전자기학] 15. 전류 | Electric Current (0) | 2023.10.12 |
| [물리학-전자기학] 13. 정전용량(커패시턴스) | Capacitance (1) (0) | 2023.10.09 |
| [물리학-전자기학] 12. 적용: 전위 | Applications: EP (1) (0) | 2023.10.09 |
| [물리학-전자기학] 40. 번개 | Lightning (0) | 2023.09.26 |