
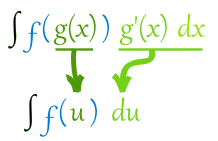
적분법에 들어가기에 앞서 먼저 미적분학의 미분법에 대해 간단히 복습하자.

미분법과 마찬가지로 적분에서도 합성함수를 적분하는 여러 가지 전략이 있다.
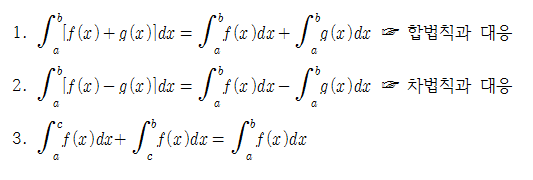
곱법칙(몫법칙을 포함해), 그리고 연쇄법칙과 대응되는(corresponds to) 적분법들도 존재하는데 대응관계는 다음과 같다.
1. 부분적분(integration by parts): 곱법칙에 대응한다.
2. 치환적분(integration by substitution): 연쇄법칙에 대응한다.
치환적분
치환적분은 연쇄법칙과 유사한 방법의 적분법으로 연쇄법칙에서의 내부함수의 치환 요령을 따른다.
[1] 내부함수를 u로 치환한다.
[2] du/dx=g'(x)를 구한다.
[3] 적분식에서 dx를 다음과 같이 바꿔 쓸 수 있다. ⇒ dx=du/g'(x)
[4] u를 포함한 내부함수를 적분하고, 구한 최종 값의 u는 다시 원래의 값(치환 이전의 값)으로 환원한다.
EXAMPLE. 부정적분의 치환적분
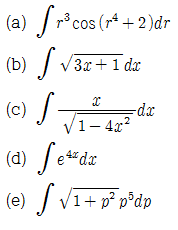
□
치환적분의 의의: 치환적분은 상대적으로 복잡하게 보이는 적분을 좀 더 간단한 형태의 적분으로 바꾸는 것이 목적이다. 그리고 이를 위해 원래의 변수를 새로운 변수 u로 치환하는 방법을 선택한다. 치환법칙의 핵심은 적당한 치환 함수를 선택하는 것이다.
- 만약 치환 함수의 전개가 어려울 경우, 다른 함수를 치환하여 재시도한다.
- 치환한 변수(문자) u로 피적분 함수를 모두 표현할 수 있다. (단, 피적분 함수 내의 상수나 숫자는 치환대상으로부터 제외한다.)
부정적분 치환적분
만약 u=g(x)가 구간 I를 치역으로 갖는 미분가능함수이고, f가 I위에서 연속이면 다음과 같다.
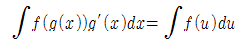
■
이제 정적분의 치환적분을 알아보자.
정적분 치환적분
만약 g'이 [a, b]에서 연속하고, f가 u=g(x)의 치역에 연속한다면,
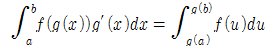
■
- 문제에서 주어지는 상한과 하한 값은 x에 대한 것이다. 따라서 피적분함수를 u로 치환할 때, x에 대한 상한과 하한 값 역시 수정해야 한다.
EXAMPLE. 정적분 치환적분
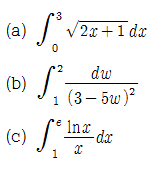
□
※ Substitution for Integrals: corresponding to the chain rule for derivatives
[1] Suppose that F(u) is an antiderivative of f(u):
∫f(u)du = F(u)+C
[2] Assume that u=u(x) is a differentiable function and using the chain rule:
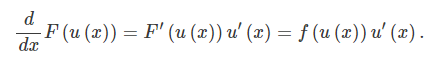
[3] Integrating both sides gives:
∫f(u(x))u'(x)dx = F(u(x))+C
[4] Hence,
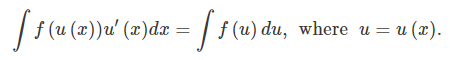
This is the substitution rule formula for indefinite integrals.
- The integral on the left side is in terms of the variable x
- The integral on the right side is in terms of the variable u
'미분적분학 > 적분' 카테고리의 다른 글
| 【미분적분학 2】 Chapter 8. 삼각함수적분 (0) | 2024.11.22 |
|---|---|
| 【미분적분학 2】 Chapter 7. 부분적분 (0) | 2024.11.21 |
| 【미분적분학 2】 Chapter 5. 부정적분 (0) | 2024.11.18 |
| 【미분적분학 2】 Chapter 4. 미적분학의 기본정리 (0) | 2024.11.17 |
| 【미분적분학 2】 Chapter 3. 정적분: 정의와 의미 (0) | 2024.11.01 |