
곡선 함수의 넓이를 구할 때, 직사각형의 넓이를 설정하는 방법으로 총 3가지를 알아보았다. 특히, 표본점의 근사식은 곡선의 길이, 입체의 부피, 질량중심, 압력에 의한 힘(force) 등 다양한 물리량을 구하는 문제에 활용된다. 그러므로 이러한 형태의 극한은 특별한 이름과 기호를 붙일 수 있다.
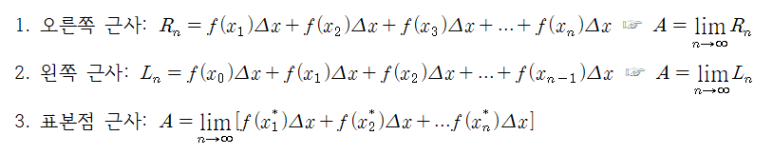
정적분의 정의 | Definition of Definite Integral

단, 극한이 존재하고 표본점을 어떤 식으로 잡더라도 그 값은 서로 동일하다고 가정한다. 그리고 이 극한이 존재할 때 f는 [a, b] 구간에서 적분가능(integrable)이라 한다.
■
적분법
Integration
정적분에 나온 적분기호 ∫(인테그랄, integral)은 적분법에 쓰이는 대표 기호로 각각의 의미를 알아보자.
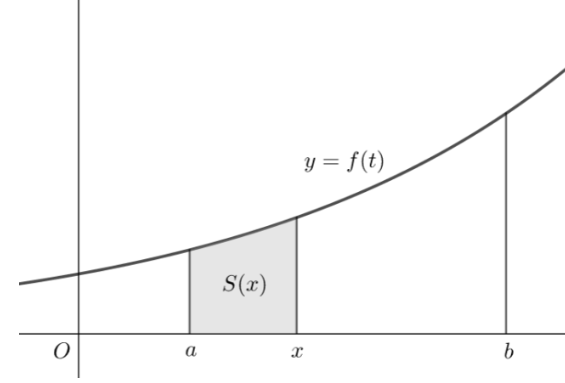
적분법으로 면적 S(x)[그림 1]는 다음과 같이 표현할 수 있다. (단, 그래프의 가로축은 t축이라 정한다.)
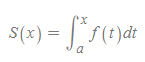
- ∫: 적분기호(integral, integral sign)
- f(t): 피적분함수(integrand)
- a, x: 적분기호 속 적분한계(limits of integration)
- a: 하한(lower limit)
- x: 상한(upper limit)
- dt: 독립변수가 t임을 표시
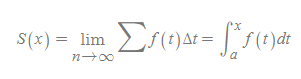
적분법으로 작성하면서 리만합의 (1)직사각형 개수와 (2)Δx는 각각 (1)하한-상한 구간과 (2)dx 표시로 전환되었다.

알짜 넓이
Net Area
함수 f가 양의 값을 가질 때, 리만합의 직사각형들은 아래와 같이 해석된다.

[그림 1]과 같은 함수 모양은 f가 모두 양의 값을 갖는다. 하지만 [그림 2]와 같이 양의 면적과 음의 면적을 모두 가지는 경우, 리만합은 x축을 기점으로 위의 면적에 아래 면적을 모두 합한 결과 값이 된다.
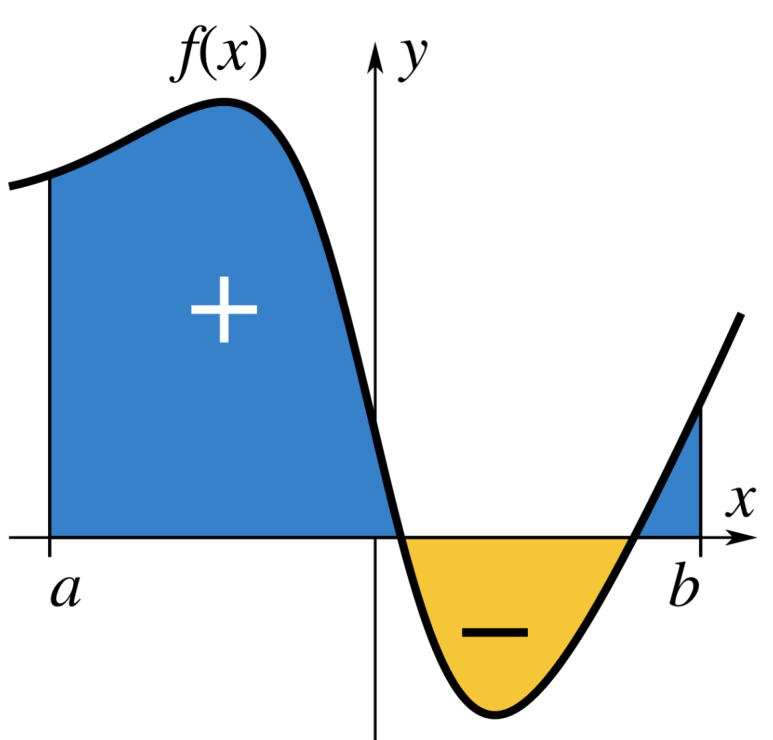
- x축 아래 놓인 직사각형들의 넓이는 음수부호를 가지므로, 리만합은 위의 면적의 총합에서 아래 면적의 총합을 뺀 값과 같다.
- 즉, 리만합의 변형 표현인 적분법 또한 하한-상한 구간에 대한 알짜 넓이(순넓이, net area) 값으로 해석될 수 있다.

오늘날 일반적으로 사용되는 적분 기호 ∫는 독일의 철학자 라이프니츠(Gottfried W. Leibniz, 1646-1716)의 공책에 최초로 작성(1675.11.11)되었으며, 그는 y=f(x)의 그래프에서 밑 면적을 계산하는 데 합을 뜻하는 라틴어 Summa의 S를 길게 늘인 기호로 활용했다.

'미분적분학 > 적분' 카테고리의 다른 글
| 【미분적분학 2】 Chapter 6. 치환적분 (0) | 2024.11.20 |
|---|---|
| 【미분적분학 2】 Chapter 5. 부정적분 (0) | 2024.11.18 |
| 【미분적분학 2】 Chapter 4. 미적분학의 기본정리 (0) | 2024.11.17 |
| 【미분적분학 2】 Chapter 2. 표본점과 리만합 (0) | 2024.10.31 |
| 【미분적분학 2】 Chapter 1. 적분: 넓이 구하기 (0) | 2024.10.30 |