
앞선 챕터에서 우리는 오른쪽 근사와 왼쪽 근사를 알아보았다. 그리고 서로 다른 끝점에 의해 아래와 같은 대소 관계를 가짐을 확인했다.

이제는 이 아이디어를 확장하여 일반적인 영역 S에 적용할 수 있는 방법론을 알아보자.

[1] 먼저 어떤 함수 f(x)에 의해 생겨난 S에 대해 동일한 폭을 갖는 n개의 직사각형을 [그림 1]과 같이 나눈다. 단, 여기서는 오른쪽 끝점들(right endpoints)로 설정한 면적에 설명을 한정한다.

[2] 구간 [a, b](지점 a에서 b까지의 구간)의 폭 값은 b-a이고, n개의 직사각형 폭이 모두 Δx일 때, Δx는 아래 값을 만족한다.

- 구간 [a, b]의 전체 길이(폭)는 (n개의 직사각형) x (Δx)의 값과 같다.
[3] 직사각형은 [a, b]에서 n개의 부분 구간들로 서로 분할될 수 있다.

[4] [그림 2]의 오른쪽 끝점 x_1을 다음과 같이 적을 수 있다.

[5] 위를 응용하여, x_2는 다음과 같이 적을 수 있다.

⇒ 오른쪽 끝점 또는 왼쪽 끝점의 정의
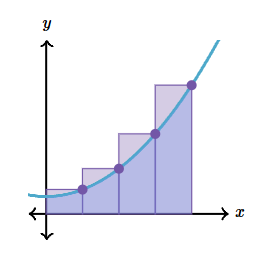
[6] i번째 곡선 아래 영역을 S_i라고 했을 때, 폭 Δx와 높이 f(x_i)인 직사각형 영역으로 근사[그림 3]시킬 수 있다.


[7] 영역 S란, 부분 직사각형 면적인 S_i의 n개의 총합에 근사한 값을 가지므로, 아래와 같이 식을 쓸 수 있다.

- 일반적인 영역 S에 적용시키는 방법론의 적용 그림이 right endpoints를 따르기 때문에 근사된 넓이 합은 R로 표현하였다.
표본점
Sample Points
부분 구간의 왼쪽 끝점이나 오른쪽 끝점 대신 i번째 직사각형의 높이를 i번째의 부분구간 내에 있는 임의의 점 x_i^*에 대한 f의 값으로 선택할 수 있다. 이때 x_i^*를 표본점[그림 4]이라 한다.
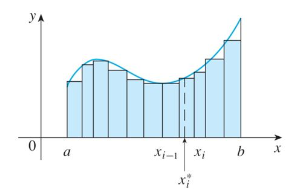

임의의 표본점은 대개는 left endpoint와 right endpoint의 중간 지점이고, 이에 따라 표본점에 따른 넓이의 정의를 아래와 같이 쓸 수 있다.
표본점 넓이 정의
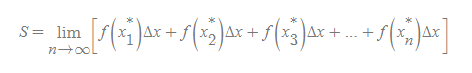
■
참고로 [그림 3]에 따르면, 왼쪽 근사와 오른쪽 근사 넓이는 다음과 같다.
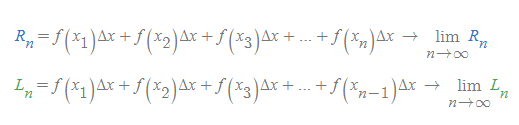
R_n과 L_n은 그 자체로 수많은 항을 가지므로, 이를 간결하게 표현하게 위해 시그마 기호를 도입한다.
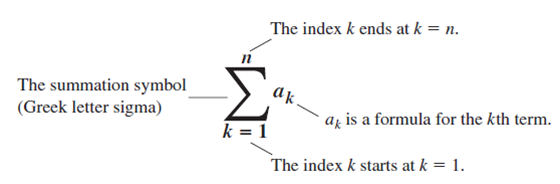
- 시그마 기호의 정의: k=1에서 시작해 k=n까지의 a_k의 모든 값을 더하시오.
- 시그마 기호를 이용해 오른쪽 끝점과 왼쪽 끝점 극한 넓이 값을 다음과 같이 정리할 수 있다.
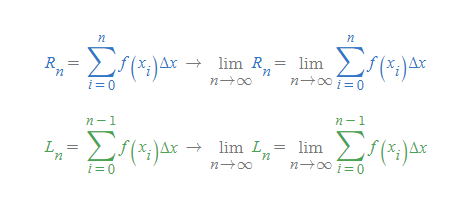
따라서 표본점 넓이 정의도 아래와 같이 간략하게 표현할 수 있다.
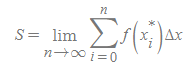
리만합
Riemann Sum

위의 예시와 같은 근사 넓이 결과를, 독일의 수학자 베른하르트 리만(Bernhard Riemann, 1826-1866)의 이름을 딴 리만합으로 정의한다.
왼쪽 리만합 규칙(Left Rule)
리만합 규칙은 앞서 설명한 면적 계산에 관한 직사각형 근사법으로서, Δx의 폭을 가진 직사각형의 수를 늘릴수록 더욱 근사값이 좋아짐을 전제한다. 면적에 대한 직사각형 생성 방법에 따라 리만합의 유형이 나뉘는데, 왼쪽 리만합 규칙은 직사각형의 왼쪽 모서리와 곡선이 만나도록 하는 것[그림 5]이다.
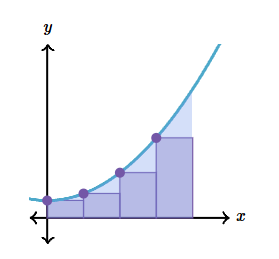
왼쪽 리만합의 면적 값은 다음과 같다.
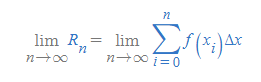
오른쪽 리만합 규칙(Right Rule)
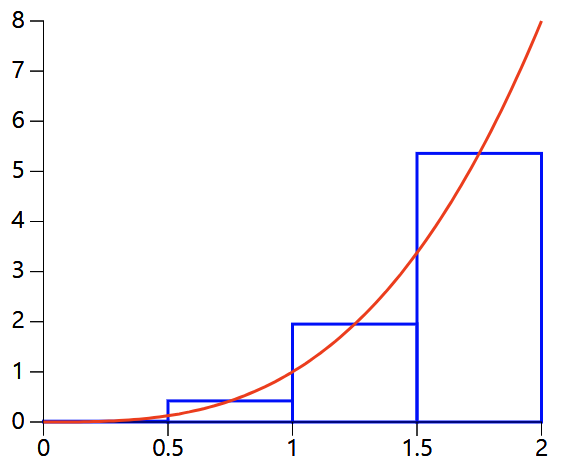
직사각형을 만드는 다른 방법으로 직사각형의 오른쪽 모서리를 곡선에 만나도록 할 수 있다[그림 6]. 그리고 이를 오른쪽 리만합 규칙이라 한다.
오른쪽 리만합의 면적 값은 다음과 같다.
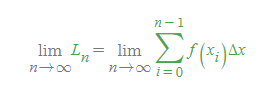
중점 리만합 규칙(Midpoint Rule)
직사각형을 만드는 또 다른 방법은 직사각형의 중간 지점을 곡선에 만나도록 그리는 것이다. 여기서 표현하는 중간지점이란 왼쪽 끝점과 오른쪽 끝점 중간에 위치한 중점(midpoint)으로, [그림 7]과 같이 직사각형이 놓여진다.
'미분적분학 > 적분' 카테고리의 다른 글
| 【미분적분학 2】 Chapter 6. 치환적분 (0) | 2024.11.20 |
|---|---|
| 【미분적분학 2】 Chapter 5. 부정적분 (0) | 2024.11.18 |
| 【미분적분학 2】 Chapter 4. 미적분학의 기본정리 (0) | 2024.11.17 |
| 【미분적분학 2】 Chapter 3. 정적분: 정의와 의미 (0) | 2024.11.01 |
| 【미분적분학 2】 Chapter 1. 적분: 넓이 구하기 (0) | 2024.10.30 |