Herald-Lab
【미분적분학 2】 Chapter 1. 적분: 넓이 구하기 본문

아르키메데스의 소진법
Method of Exhaustion

현대적인 적분 개의 기원은 고대 그리스 시대의 수학자 아르키메데스(Archimedes of Syracuse, B.C. 287 - B.C. 212)가 곡선을 가진 도형의 면적과 부피를 구함에 있어, 오늘날의 적분과 매우 유사한 방법을 사용한 데서 출발한다.
- 아르키메데스의 소진법: 아르키메데스는 [그림 1]과 같이, 포물선을 가로지르는 특정한 직선에 의해 경계를 갖춘 면적(parabolic segment)의 넓이를 구하는 것을 탐구했는데, 이에 대한 해결책으로 그는 [그림 2]와 같은 포물선에 내접한 삼각형 면적을 반복적으로 만들어 나가는 '소진법(消盡法, method of exhaustion)'을 구상했다.
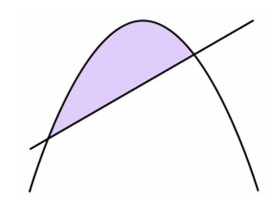
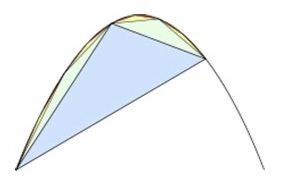
[그림 2]와 같이 포물선에 내접한 첫 삼각형의 공백을 없애기 위해, 계속해서 내접하는 삼각형을 만들어 가야 하는데, 그들 간에는 기하학적으로 특수한 규칙이 성립하고, 이들은 현대적인 표현으로 '무한등비급수의 합(infinite geometric series)'으로 표현된다.
카발리에리의 원리
Cavalieri's Idea
1622년 이탈리아의 수학자 보나벤투라 카발리에리(Bonaventura F. Cavalieri, 1598-1647)가 무한의 개념을 도입하여 곡선으로 둘러싸인 도형의 면적은 매우 폭이 좁은 직사각형들의 면적의 합이라고 주장한다.
- 카발리에리의 원리: 두 평면 도형을 서로 평행한 직선으로 자를 때, 두 도형을 지나는 선분의 길이가 항상 같다면, 두 도형의 넓이는 같다. [그림 3]
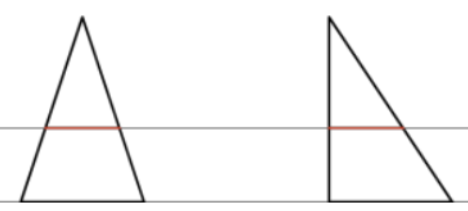
두 평면 도형을 어떠한 직선에 평행한 직선으로 나누었을 때, 도형 내부의 선분 길이가 항상 같으면 이 두형의 넓이도 항상 같다.
위의 내용을 응용하면, 현대의 정적분 개념은 '어떠한 곡선 영역에서라도 무한히 잘게 쪼개진 너비가 같고 높이만 다른 직사각형의 전체 넓이 합'으로 정의할 수 있다.
곡선 함수 아래 넓이 구하기
직사각형이나 삼각형의 넓이는 이미 공식을 통해 매우 쉽게 구할 수 있다. 하지만 f(x)=x^2인 밑면적[그림 5]을 구하는 것은 그리 쉬운 문제가 아니다.
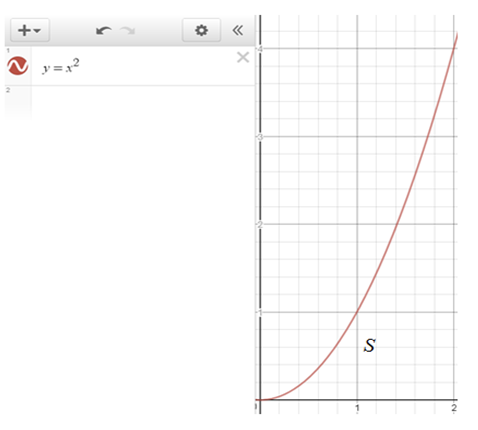
하지만 역사적인 인물들의 아이디어를 빌려, 곡선을 갖는 밑면적을 구하기 위해서 우리는 현재 아래와 같은 절차를 따른다.
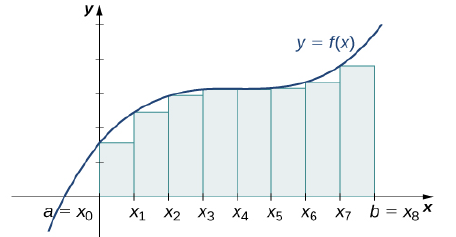
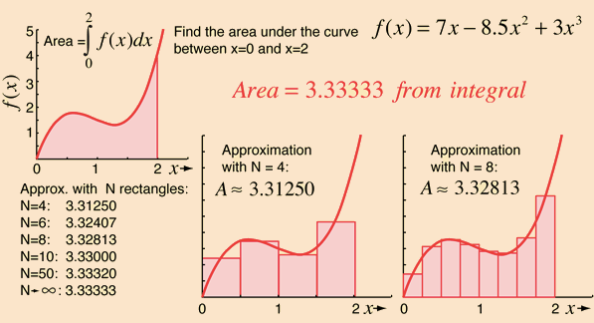
[1] 곡선함수의 그래프 영역 S를 너비가 같은 직사각형들로 잘게 쪼갠다.
[2] 직사각형을 더 잘게 쪼갤수록 이들의 전체 합은 구하려는 S의 값과 더욱 근사한다.
[3] 직사각형의 수를 무한히 늘렸다 가정하여, '직사각형 넓이의 극한'을 구한다.
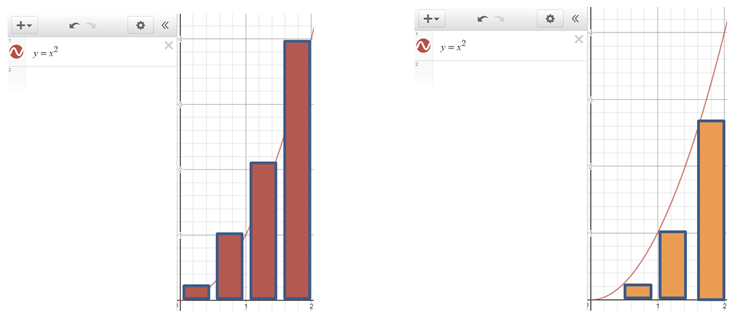
직사각형의 넓이를 설정할 때는 2가지의 방법[그림 6]을 고를 수 있다.
- 오른쪽 근사: 오른쪽 끝점을 기준으로 전체 영역을 직사각형의 묶음들로 쪼갠다. ⇒ 빨간색
- 왼쪽 근사: 왼쪽 끝점을 기준으로 전체 영역을 직사각형의 묶음들로 쪼갠다. ⇒ 주황색
여기서 끝점(endpoint)이란, [그림 7]과 같은 지점이다.
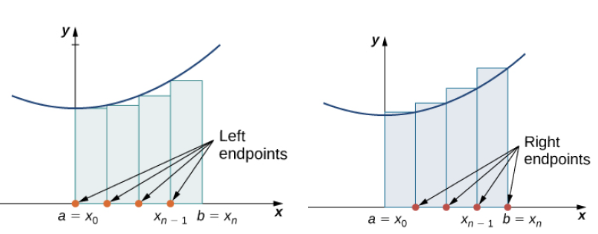
- x축을 기준으로 한 직사각형 영역에서 왼쪽 지점을 left endpoint라고 한다.
- x축을 기준으로 한 직사각형 영역에서 오른쪽 지점을 right endpoint라고 한다.
오른쪽 근사와 왼쪽 근사를 한 면적의 총합을 각각 R_n, L_n(단, n은 직사각형의 개수)이라 정의한다.
- 표면적으로 왼쪽 근사의 경우 오른쪽 근사보다 직사각형 개수가 하나 모자란데[그림 6], 그 이유는 f(x)=x^2 그래프의 시작점에서 왼쪽 끝점의 값은 0이므로 전체 직사각형은 0의 넓이를 갖기 때문이다. 둘은 같은 폭의 직사각형을 상정하고 f(x)아래 배치되기 때문에, 왼쪽 근사의 경우에도 넓이가 0인 직사각형을 포함해 4개의 직사각형이 있다고 가정한다.
- 왼쪽 근사와 오른쪽 근사는 그래프에 놓인 위치 차이로 인해 [그림 8]과 같이 S 영역의 값을 서로 다르게 측정한다.
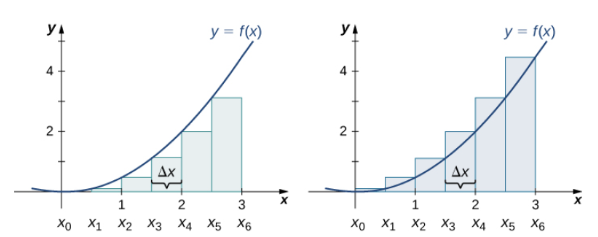
따라서 오른쪽 근사와 왼쪽 근사의 총합과 실제 영역 간에는 아래와 같은 대소관계를 갖는다.
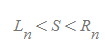
그리고 직사각형의 숫자 n을 증가시킬수록[그림 9], 아래와 같은 식을 만족한다.
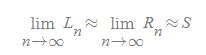
함수 f(x)가 주어질 때, 극한의 개념을 활용해 미분을 구할 수 있다. 마찬가지로 함수의 미분이 주어질 때도 f(x)를 구할 수 있는데 이는 적분이라는 과정을 통해 가능하다.
'미분적분학 > 적분' 카테고리의 다른 글
| 【미분적분학 2】 Chapter 6. 치환적분 (0) | 2024.11.20 |
|---|---|
| 【미분적분학 2】 Chapter 5. 부정적분 (0) | 2024.11.18 |
| 【미분적분학 2】 Chapter 4. 미적분학의 기본정리 (0) | 2024.11.17 |
| 【미분적분학 2】 Chapter 3. 정적분: 정의와 의미 (0) | 2024.11.01 |
| 【미분적분학 2】 Chapter 2. 표본점과 리만합 (0) | 2024.10.31 |





